Cauchy< C > Struct Template Reference

Cauchy bound. More...

#include <univariate_bounds.hpp>

List of all members.

Public Member Functions

template<class Poly > C lower_bound (const Poly &f) const
Computes the Cauchy lower bound on the first positive root as a power of 2.
template<class Poly > long lower_power_2 (const Poly &f) const
template<> double upper_bound (const Poly &p)

Static Public Member Functions

template<class Poly > static C upper_bound (const Poly &p)
Computes the Cauchy root bound.

Detailed Description

template<class C>
struct mmx::Cauchy< C >

Cauchy bound.

Definition at line 161 of file univariate_bounds.hpp.

Member Function Documentation

C lower_bound ( const Poly & f ) const [inline]

Computes the Cauchy lower bound on the first positive root as a power of 2.

Parameters:

f

Univariate polynomial

Definition at line 209 of file univariate_bounds.hpp.

References mmx::abs(), mmx::bit_size(), C, mmx::degree(), mmx::univariate::degree(), and mmx::sign().

00211 00212 00213 00214 00215 00216 00217 00218 00219 00220         } 00221       } 00222 00223 00224 00225 00226 00227 00228 00229 00230 00231 00232 00233 00234 00235 00236 00237 00238 00239 00240           } 00241 00242 00243 00244 00245           } 00246         } 00247       } 00248 00249 00250 00251     }

class="fragment">00210 { using univariate::degree; typedef C RT; long deg = degree( f); long l = 0; for (int i = 1; i <= deg; ++i) { if ( sign( f[i]) * sign( f[0]) < 0 ) { ++l; long ba0 = bit_size(f[0]) - 1; /* puiss de 2 < an */ bool bound_set = false; long K = 0; for (int i = 1; i <= deg; ++i) { if ( sign( f[i]) * sign( f[0]) < 0 ) { long bai = bit_size( RT( l * f[i])) - 1; long p = bai - ba0 - 1 ; long k = i; long q = p / k; long r = p % k; long rq = 0; if (r <= k-2) { rq = q + 1; } else { rq = q + 2; if ( (bound_set == false) || (K < rq) ) { K = rq; bound_set = true; if ( K < 0 ) {return pow2<RT>( abs( K) );} return 0;

long lower_power_2 ( const Poly & f ) const [inline]

Definition at line 255 of file univariate_bounds.hpp.

References mmx::abs(), mmx::bit_size(), mmx::degree(), mmx::univariate::degree(), and mmx::sign().

00256     {
00257       using univariate::degree;
00258 
00259       typedef typename Poly::value_type RT;
00260 
00261       long deg = degree( f);
00262       long l = 0;
00263 
00264       for (int i = 1; i <= deg; ++i) {
00265         if ( sign( f[i]) * sign( f[0]) < 0 ) {
00266           ++l;
00267         }
00268       }
00269 
00270       long ba0  = bit_size(f[0]) - 1; /* puiss de 2 < an */
00271       bool bound_set = false;
00272       long K = 0;
00273 
00274       for (int i = 1; i <= deg; ++i) {
00275         if ( sign( f[i]) * sign( f[0]) < 0 ) {
00276           long bai  = bit_size( RT( l * f[i])) - 1;
00277           long p = bai - ba0 - 1 ;
00278           long k = i;
00279           long q = p / k;
00280           long r = p % k;
00281 
00282           long rq = 0;
00283           if (r <= k-2) {
00284             rq = q + 1;
00285           } else {
00286             rq = q  + 2;
00287           }
00288 
00289           if ( (bound_set == false) || (K < rq) ) {
00290             K = rq;
00291             bound_set = true;
00292           }
00293         }
00294       }
00295       if ( K < 0 ) { abs( K);}
00296 
00297       return -1;
00298     }

double upper_bound ( const Poly & p ) [inline]

Definition at line 304 of file univariate_bounds.hpp.

References mmx::abs(), mmx::univariate::lcoeff(), mmx::vctops::max(), and mmx::numerics::rnd_up().

00305   {
00306     typedef typename Poly::value_type coeff_t;
00307     numerics::rounding<double> rnd( numerics::rnd_up() );
00308     //using std::abs;
00309     coeff_t M=0;
00310     for(unsigned i=0;i< p.size(); i++) M = std::max(M, coeff_t(abs(p[i])));
00311     //    abs_max<coeff_t> M = std::for_each(p.begin(), p.end()-1, abs_max<coeff_t>());
00312 
00313     coeff_t an = coeff_t(abs(univariate::lcoeff(p)));
00314     //std::cout <<M<<" "<<an<<" "<<std::endl;
00315 
00316     double res=as<double>(coeff_t(M/an)) + 1;
00317     //    std::cout <<res<<std::endl;
00318     return res;
00319   }

static C upper_bound ( const Poly & p ) [inline, static]

Computes the Cauchy root bound.

Parameters:

p

Univariate polynomial

Poly is the type of the polynomial. C is the type of the result.

If the polynomial p is in the monomial basis is of the form

$p(x) = a_{0} + a_{1} x+ \cdots + a_{d}\, x^d,$

the Cauchy bound on the modul of the roots of 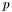$p$ is

$1 + max{|a_{0}|,...,|a_{d-1}|}/|a_{d}|$

See also:: bound_root

Definition at line 186 of file univariate_bounds.hpp.

References mmx::abs(), C, mmx::univariate::lcoeff(), and abs_max< T >::max.

Referenced by mmx::bound_root().

00187     {
00188           //std::cout<< "Cauchy" <<std::endl;
00189           typedef typename Poly::value_type     RT;
00190           typedef typename texp::rationalof<RT>::T rational;
00191 
00192           //using std::abs;
00193           abs_max<RT> M = std::for_each(p.begin(), p.end()-1, abs_max<RT>());
00194           RT an =  abs(lcoeff(p));
00195           //std::cout<< "Max "<< M.max <<" " <<an<< std::endl;
00196           //      rational val= rational(M.max)/an + rational(1);
00197           C res= C(M.max/an) + C(1);
00198           //      C res; let::assign(res, val);
00199           return res;
00200     }

The documentation for this struct was generated from the following file:

include/realroot/univariate_bounds.hpp