AkritasBound< RT > Struct Template Reference

#include <univariate_bounds.hpp>

List of all members.

Static Public Member Functions

• template<typename Poly > static RT lower_bound (const Poly &f)
• template<typename Poly > static long lower_power_2 (const Poly &f)

---

Detailed Description

template<class RT>
struct mmx::AkritasBound< RT >

A 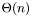time algorithm for computing a lower bound. It is based upon an upper bound by Akritas et al. that returns a value some what better than Kioustelidis' bound, but is not better than the bound by Hong. The idea is to pair the positive and negative coefficients in a certain manner. Assume the constant coefficient is not zero and there is at least one sign variation in the coefficients.

Definition at line 407 of file univariate_bounds.hpp.

---

Member Function Documentation

static RT lower_bound

(

const Poly &

f

)

[inline, static]

Definition at line 411 of file univariate_bounds.hpp.

References mmx::abs(), mmx::bit_size(), mmx::degree(), mmx::univariate::degree(), and mmx::sign().

Referenced by solver_cffirst< Real, POL >::all_roots(), and solver_cffirst< Real, POL >::first_root().

    {
      using univariate::degree;

      //    std::cout <<"Poly is " << f << std::endl;
      typedef std::pair<RT, int>        Coeff_deg;
      Coeff_deg T1, T2;

      unsigned deg=degree(f);
      int s=sign(f[0]);//, len;
      long B=0;// The logarithm of the bound to be returned
      bool boundSet=false;// The bound is not set initially
      long temp,q;
      int posCounter=0, negCounter=0, nPosCounter=0;
      // The coefficients from posCounter to negCounter-1 have the same sign
      // as f[0]; the coefficients from negCounter to nPosCounter-1 have the
      // opposite sign of f[0].
      std::queue< Coeff_deg > Neg;// Queue that stores the negative (between
      // negCounter and nPosCounter) coefficients.
      std::stack< Coeff_deg > Pos; // Stack that stores the positive (between
      // posCounter and negCounter) coefficients.

      int l1, l2;// size of the above two queues

      while(posCounter != int(deg+1)){
        // Find the first change in sign larger than posCounter and assign negCounter
        // to this value. If no such sign variation occurs then
        // set negCounter to -1.
        negCounter = -1;// By default there is no such coefficient
        //Pos.push(Coeff_deg(RT(f[posCounter]), posCounter));// Push the first "positive" coefficient
        Pos.push(Coeff_deg(RT(f[posCounter]), posCounter));// Push the first "positive" coefficient
        for(unsigned i=posCounter + 1;i <= deg; i++){
          if(sign(f[i]) * s < 0){
            negCounter=i; break;
          }
          if(sign(f[i]) *s > 0){// Store the list of "positive" coefficients
            //Pos.push(Coeff_deg(RT(f[i]), i));// Note the actual degree is deg-i, but
            // later we subtract degrees so we store only i
            Pos.push(Coeff_deg(RT(f[i]), i));
          }
        }
        if(negCounter == -1){
          //    std::cout <<"Returning the lower bound " << B << std::endl;
          if ( B < 0 )
            return pow2<RT>( abs(B) );
          else
            return 0;
        }
        // Now find the next coefficient that has the same sign as f[0].
        nPosCounter = deg+1;// By default this is deg+1
        Neg.push(Coeff_deg(RT(f[negCounter]), negCounter));
        for(unsigned i=negCounter + 1;i <= deg; i++){
          if(sign(f[i]) * s > 0){
            nPosCounter=i; break;
          }
          if(sign(f[i]) *s < 0)// Store the list of "negative" coefficients
            Neg.push(Coeff_deg(RT(f[i]), i));
        }

        //      std::cout <<" Assigning to the queues done" << std::endl;
        // Start computing the bound
        // If the number of "positive" terms from posCounter to negCounter -1 are
        // greater or equal to  the number of "negative" terms from negCounter to
        // nPosCounter -1 then we have the straightforward matching of "negative"
        // coefficients with the "positive" ones.
        l1 = Neg.size(); l2 = Pos.size();
        if(l2 >= l1){
          //    std::cout <<"Pos length " << l2 << " greater than Neg length "
          //              << l1 << std::endl;
          // or equally negCounter - posCounter >= nPosCounter - negCounter
          for(int i=0; i < l1; i++){
            T1= Neg.front(); Neg.pop();
            //T2= Pos.front(); Pos.pop();
            T2=Pos.top();Pos.pop();
            //    std::cout <<"Neg coeff " << T1.first << " Pos coeff " << T2.first
            //              << " Deg difference " << T1.second - T2.second
            //              << std::endl;
            temp = bit_size( T1.first ) - bit_size( T2.first ) - 1;
            q = temp/(T1.second - T2.second);
            //    std::cout << "Difference between logs " << temp
            //              << " temporary bound value " << B << std::endl;
            if(!boundSet || B < q + 2){// Choose the maximum
              boundSet = true;
              B = q+2;
            }
          }
        }else{//Else split the coefficient f[posCounter] to compensate for
          // the paucity of "positive" terms and then do the matching.
          //    std::cout <<" Pos length "<< l2 << " smaller than Neg length "
          //              << l1 << std::endl;

          //T2=Pos.front(); Pos.pop();
          T2= Pos.top();Pos.pop();
          for(int i=0; i <= l1-l2; i++){
            T1= Neg.front(); Neg.pop();
            temp = bit_size( T1.first ) - bit_size( T2.first ) + bit_size(RT(l1-l2+1)) - 1;
            q = temp/(T1.second-T2.second);
            if(!boundSet || B < q + 2){// Choose the maximum
              boundSet = true;
              B = q+2;
            }
          }
          //    std::cout <<" Splitting the leading coefficient done" << std::endl;
          l1 = Neg.size();// Now the size of Neg and Pos should be the same
          for(int i=0; i < l1; i++){
            T1= Neg.front(); Neg.pop();
            //T2= Pos.front(); Pos.pop();
            Pos.pop();
            temp = bit_size( T1.first ) - bit_size( T2.first ) - 1;
            q = temp/(T1.second - T2.second);
            if(!boundSet || B < q + 2){// Choose the maximum
              boundSet = true;
              B = q+2;
            }
          }
        }// end else
        //      std::cout <<" Matching the coefficients done" << std::endl;
        posCounter = nPosCounter; Neg.empty(); Pos.empty();
      }//end while
      //    std::cout <<"Returning the lower bound " << B << std::endl;
      if ( B < 0 ) return pow2<RT>( abs(B) );
      return 0;
    }

static long lower_power_2

(

const Poly &

f

)

[inline, static]

Definition at line 537 of file univariate_bounds.hpp.

References mmx::abs(), mmx::bit_size(), mmx::degree(), mmx::univariate::degree(), and mmx::sign().

      {
        using univariate::degree;

          //    std::cout <<"Poly is " << f << std::endl;
          typedef std::pair<RT, int>    Coeff_deg;
          Coeff_deg T1, T2;

          unsigned deg=degree(f);
          int s=sign(f[0]);//, len;
          long B=0;// The logarithm of the bound to be returned
          bool boundSet=false;// The bound is not set initially
          long temp,q;
          int posCounter=0, negCounter=0, nPosCounter=0;
          // The coefficients from posCounter to negCounter-1 have the same sign
          // as f[0]; the coefficients from negCounter to nPosCounter-1 have the
          // opposite sign of f[0].
          std::queue< Coeff_deg > Neg;// Queue that stores the negative (between
          // negCounter and nPosCounter) coefficients.
          std::stack< Coeff_deg > Pos; // Stack that stores the positive (between
          // posCounter and negCounter) coefficients.

          int l1, l2;// size of the above two queues

          while(posCounter != int(deg+1)){
              // Find the first change in sign larger than posCounter and assign negCounter
              // to this value. If no such sign variation occurs then
              // set negCounter to -1.
              negCounter = -1;// By default there is no such coefficient
              //Pos.push(Coeff_deg(RT(f[posCounter]), posCounter));// Push the first "positive" coefficient
              Pos.push(Coeff_deg(RT(f[posCounter]), posCounter));// Push the first "positive" coefficient
              for(unsigned i=posCounter + 1;i <= deg; i++){
                  if(sign(f[i]) * s < 0){
                      negCounter=i; break;
                  }
                  if(sign(f[i]) *s > 0){// Store the list of "positive" coefficients
                      //Pos.push(Coeff_deg(RT(f[i]), i));// Note the actual degree is deg-i, but
                      // later we subtract degrees so we store only i
                      Pos.push(Coeff_deg(RT(f[i]), i));
                  }
              }
              if(negCounter == -1){
                  //    std::cout <<"Returning the lower bound " << B << std::endl;
                  if ( B < 0 ) return abs( B);
                  else return -1;
              }
              // Now find the next coefficient that has the same sign as f[0].
              nPosCounter = deg+1;// By default this is deg+1
              Neg.push(Coeff_deg(RT(f[negCounter]), negCounter));
              for(unsigned i=negCounter + 1;i <= deg; i++){
                  if(sign(f[i]) * s > 0){
                      nPosCounter=i; break;
                  }
                  if(sign(f[i]) *s < 0)// Store the list of "negative" coefficients
                      Neg.push(Coeff_deg(RT(f[i]), i));
              }

              //      std::cout <<" Assigning to the queues done" << std::endl;
              // Start computing the bound
              // If the number of "positive" terms from posCounter to negCounter -1 are
              // greater or equal to  the number of "negative" terms from negCounter to
              // nPosCounter -1 then we have the straightforward matching of "negative"
              // coefficients with the "positive" ones.
              l1 = Neg.size(); l2 = Pos.size();
              if(l2 >= l1){
                  //    std::cout <<"Pos length " << l2 << " greater than Neg length "
                  //              << l1 << std::endl;
                  // or equally negCounter - posCounter >= nPosCounter - negCounter
                  for(int i=0; i < l1; i++){
                      T1= Neg.front(); Neg.pop();
                      //T2= Pos.front(); Pos.pop();
                      T2=Pos.top();Pos.pop();
                      //          std::cout <<"Neg coeff " << T1.first << " Pos coeff " << T2.first
                      //                    << " Deg difference " << T1.second - T2.second
                      //                    << std::endl;
                      temp = bit_size( T1.first ) - bit_size( T2.first ) - 1;
                      q = temp/(T1.second - T2.second);
                      //          std::cout << "Difference between logs " << temp
                      //                    << " temporary bound value " << B << std::endl;
                      if(!boundSet || B < q + 2){// Choose the maximum
                          boundSet = true;
                          B = q+2;
                      }
                  }
              }else{//Else split the coefficient f[posCounter] to compensate for
                  // the paucity of "positive" terms and then do the matching.
                  //    std::cout <<" Pos length "<< l2 << " smaller than Neg length "
                  //              << l1 << std::endl;

                  //T2=Pos.front(); Pos.pop();
                  T2= Pos.top();Pos.pop();
                  for(int i=0; i <= l1-l2; i++){
                      T1= Neg.front(); Neg.pop();
                      temp = bit_size( T1.first ) - bit_size( T2.first ) + bit_size(RT(l1-l2+1)) - 1;
                      q = temp/(T1.second-T2.second);
                      if(!boundSet || B < q + 2){// Choose the maximum
                          boundSet = true;
                          B = q+2;
                      }
                  }
                  //    std::cout <<" Splitting the leading coefficient done" << std::endl;
                  l1 = Neg.size();// Now the size of Neg and Pos should be the same
                  for(int i=0; i < l1; i++){
                      T1= Neg.front(); Neg.pop();
                      //T2= Pos.front(); Pos.pop();
                      Pos.pop();
                      temp = bit_size( T1.first ) - bit_size( T2.first ) - 1;
                      q = temp/(T1.second - T2.second);
                      if(!boundSet || B < q + 2){// Choose the maximum
                          boundSet = true;
                          B = q+2;
                      }
                  }
              }// end else
              //      std::cout <<" Matching the coefficients done" << std::endl;
              posCounter = nPosCounter; Neg.empty(); Pos.empty();
          }//end while
          //    std::cout <<"Returning the lower bound " << B << std::endl;
          if ( B < 0 ) return abs( B);
          else return -1;

      }

---

The documentation for this struct was generated from the following file:

• include/realroot/univariate_bounds.hpp