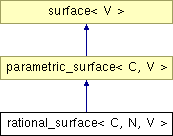
rational_surface< C, N, V > Class Template Reference

#include <rational_surface.hpp>

Inheritance diagram for rational_surface< C, N, V >:
parametric_surface< C, V > surface< V >

List of all members.

Public Types

Public Member Functions

Detailed Description

template<class C, int N = 3, class V = default_env>
class mmx::shape::rational_surface< C, N, V >

Definition at line 28 of file rational_surface.hpp.

Member Typedef Documentation

typedef use<point_def,C,V>::Point Point

Reimplemented from parametric_surface< C, V >.

Definition at line 32 of file rational_surface.hpp.

typedef point_set<C>::PointIterator PointIterator

Reimplemented from parametric_surface< C, V >.

Definition at line 33 of file rational_surface.hpp.

typedef algebraic_set<C,V>::Polynomial Polynomial

Definition at line 35 of file rational_surface.hpp.

typedef C Scalar

Reimplemented from parametric_surface< C, V >.

Definition at line 31 of file rational_surface.hpp.

Constructor & Destructor Documentation

rational_surface ( void   )  [inline]

Definition at line 37 of file rational_surface.hpp.

00037 : m_w(1) {};

rational_surface ( const Polynomial &  X,
const Polynomial &  Y,
const Polynomial &  Z,
const Polynomial &  W = 1 
) [inline]

Definition at line 40 of file rational_surface.hpp.

References rational_surface< C, N, V >::set_range().

00040                                                                                                           :
00041         ParametricSurface() {
00042         set_range(0,1,0,1);
00043         m_w=W;
00044         m_p[0]=X; m_p[1]=Y; m_p[2]=Z;
00045     }

Member Function Documentation

void add_to_domain ( const Point &  p  )  [inline]

Definition at line 199 of file rational_surface.hpp.

00199                                   {
00200     this->m_domain <<p;
00201 }

Polynomial denominator (  )  const [inline]

Definition at line 66 of file rational_surface.hpp.

00066 { return m_w; }

Point domain ( int  i  )  const [inline]

Definition at line 64 of file rational_surface.hpp.

00064 {return m_domain[i];}

Seq< typename rational_surface< C, N, V >::Point > domain ( void   )  const [inline]

Definition at line 205 of file rational_surface.hpp.

00205                    {
00206     return m_domain;
00207 }

void eval ( Scalar *  lp,
const Scalar *  u,
int  n 
) const [inline, virtual, inherited]

Definition at line 73 of file parametric_surface.hpp.

References parametric_surface< C, V >::eval().

00073                                                   {
00074     Point p;
00075     for (int i=0; i<n;i++) {
00076         this->eval(p.x(),p.y(),p.z(),u[0],u[1]);
00077         *r=p.x();r++;
00078         *r=p.y();r++;
00079         *r=p.z();r++;
00080         u+=2;
00081     }
00082 }

void eval ( Scalar &  x,
Scalar &  y,
Scalar &  z,
Scalar  u,
Scalar  v 
) const [inline, virtual]

Implements parametric_surface< C, V >.

Definition at line 143 of file rational_surface.hpp.

00143                                                                     {
00144     Scalar w=m_w(u,v);
00145     if (w != 0) {
00146         x=m_p[0](u,v)/w;
00147         y=m_p[1](u,v)/w;
00148         z=m_p[2](u,v)/w;
00149     } else {
00150         std::cerr << "Division by 0 in rational_surface::eval(Scalar& x, Scalar& y, Scalar &z, Scalar u, Scalar v const" << std::endl;
00151     }
00152 }

void eval ( Point &  p,
Scalar  u,
Scalar  v 
) const [inline]

Definition at line 87 of file rational_surface.hpp.

00087                                              {
00088     Scalar w=m_w(u,v);
00089     if (w != 0) {
00090         p.setx(m_p[0](u,v)/w);
00091         p.sety(m_p[1](u,v)/w);
00092         p.setz(m_p[2](u,v)/w);
00093     } else {
00094         std::cerr << "Division by 0 in rational_surface::eval(Point& p, Scalar u, Scalar v) const" << std::endl;
00095     }
00096 }

rational_surface< C, N, V >::Point * eval ( Scalar  u,
Scalar  v 
) const [inline]

Definition at line 80 of file rational_surface.hpp.

Referenced by rational_surface< C, N, V >::operator()().

00080                                    {
00081     Scalar w = m_w(u,v);
00082     Point* p = new Point(m_p[0](u,v)/w, m_p[1](u,v)/w, m_p[2](u,v)/w);
00083     return p ;
00084 }

void normal ( Scalar &  x,
Scalar &  y,
Scalar &  z,
Scalar  u,
Scalar  v 
) const [inline]

Definition at line 104 of file rational_surface.hpp.

References mmx::diff().

00104                                                                       {
00105     Polynomial dw0 = diff(m_w,0) , dw1 = diff(m_w,1),
00106             dx0 = diff(m_p[0],0),dx1 = diff(m_p[0],1),
00107             dy0 = diff(m_p[1],0), dy1 = diff(m_p[1],1),
00108             dz0 = diff(m_p[2],0), dz1 = diff(m_p[2],1);
00109 
00110     Scalar w=m_w(u,v);
00111     if (w != 0) {
00112 
00113         Scalar x0 = (dx0(u,v)* w - m_p[0](u,v)*dw0(u,v))/(w*w) ;
00114         Scalar x1 = (dx1(u,v)* w - m_p[0](u,v)*dw1(u,v))/(w*w);
00115         Scalar y0 = (dy0(u,v)* w - m_p[1](u,v)*dw0(u,v))/(w*w) ;
00116         Scalar y1 = (dy1(u,v)* w - m_p[1](u,v)*dw1(u,v))/(w*w);
00117         Scalar z0 = (dz0(u,v)* w - m_p[2](u,v)*dw0(u,v))/(w*w) ;
00118         Scalar z1 = (dx1(u,v)* w - m_p[2](u,v)*dw1(u,v))/(w*w);
00119 
00120         x= (y0 * z1) - (z0 * y1);
00121         y= -(x0 * z1) + (z0 * x1);
00122         z= (x0 * y1) - (y0 * x1);
00123     } else {
00124         std::cerr << "Division by 0 in rational_surface::eval(Scalar& x, Scalar& y, Scalar &z, Scalar u, Scalar v const" << std::endl;
00125     }
00126     //const scalar<double> temp = x*x + y*y + z*z;
00127     //scalar<double> norm = sqrt(temp);
00128     //Scalar temp2 = norm;
00129     //if (norm != 0) {
00130     Scalar a = sqrtf(x*x+y*y+z*z);
00131     if (a != 0) {
00132     x /= a;
00133     y /= a;
00134     z /= a;
00135 
00136 
00137    } else{
00138         std::cerr << "Division by 0 in rational_surface::eval(Scalar& x, Scalar& y, Scalar &z, Scalar u, Scalar v const" << std::endl;
00139     }
00140 
00141 }

void normal ( Point &  p,
Scalar  u,
Scalar  v 
) const [inline]

Definition at line 99 of file rational_surface.hpp.

00099                                                {
00100     normal(p[0],p[1],p[2],u,v);
00101 
00102 }

Polynomial numerator ( int  i  )  const [inline]

Definition at line 67 of file rational_surface.hpp.

00067 { return m_p[i]; }

rational_surface< C, N, V >::Point * operator() ( const Scalar &  u,
const Scalar &  v 
) const [inline]

Definition at line 187 of file rational_surface.hpp.

References rational_surface< C, N, V >::eval().

00187                                                         {
00188     return this->eval(u,v);
00189 }

void sample ( Scalar *  lp,
unsigned  m,
unsigned  n,
Scalar *  u,
Scalar *  v 
) const [inline, virtual, inherited]

Definition at line 103 of file parametric_surface.hpp.

References assert, parametric_surface< C, V >::eval(), parametric_surface< C, V >::umax(), parametric_surface< C, V >::umin(), parametric_surface< C, V >::vmax(), and parametric_surface< C, V >::vmin().

00103                                                                             {
00104     assert(m>1 && n>1);
00105     Scalar
00106             hu=(this->umax() - this->umin())/(m-1),
00107             hv=(this->vmax() - this->vmin())/(n-1);
00108 
00109     Scalar * u0 =u, su=umin(), * v0=v, sv=vmin();
00110     for (unsigned i=0; i<m;i++){ *u=su; su+=hu; u++; }
00111     for (unsigned j=0; j<n;j++){ *v=sv; sv+=hv; v++; }
00112 
00113     u=u0;
00114     for (unsigned i=0; i<m;i++,u++) {
00115         v=v0;
00116         for (unsigned j=0; j<n;j++,v++) {
00117             this->eval(r[0],r[1],r[2],*u,*v);
00118 //            *r=x;std::cout<<*r<<" ";
00119             r+=3;
00120 //            *r=y;std::cout<<*r<<" ";
00121 //            r++;
00122 //            *r=z;std::cout<<*r<<" ";
00123 //            r++;
00124 //            std::cout<<std::endl;
00125         }
00126     }
00127 }

void sample ( PointIterator  lp,
unsigned  m,
unsigned  n 
) const [inline, virtual, inherited]

Definition at line 86 of file parametric_surface.hpp.

References assert, parametric_surface< C, V >::eval(), parametric_surface< C, V >::umax(), parametric_surface< C, V >::umin(), parametric_surface< C, V >::vmax(), and parametric_surface< C, V >::vmin().

00086                                                             {
00087     assert(m>1 && n>1);
00088     Scalar
00089             hu=(this->umax() - this->umin())/(m-1), u=this->umin(),
00090             hv=(this->vmax() - this->vmin())/(n-1), v;
00091     Point pp;
00092     for (unsigned i=0; i<m;i++) {
00093         v=vmin();
00094         for (unsigned j=0; j<n;j++,p++) {
00095             this->eval(p->x(),p->y(),p->z(),u,v);
00096             v+=hv;
00097         }
00098         u+=hu;
00099     }
00100 }

void sample ( PointIterator  lp,
const Scalar *  u,
unsigned  m,
const Scalar *  v,
unsigned  n 
) const [inline, virtual, inherited]

Definition at line 130 of file parametric_surface.hpp.

References assert, and parametric_surface< C, V >::eval().

Referenced by use< ssi_def, C >::sample().

00130                                                                                                {
00131     assert(m>1 && n>1);
00132     const Scalar * v0=v;
00133 
00134     for (unsigned i=0; i<m;i++,u++) {
00135         v=v0;
00136         for (unsigned j=0; j<n;j++,p++,v++) {
00137             this->eval(p->x(),p->y(),p->z(),*u,*v);
00138         }
00139     }
00140 }

void set_denominator ( const Polynomial &  d  )  [inline]

Definition at line 70 of file rational_surface.hpp.

00070 { m_w=d; }

void set_numerator ( const Polynomial &  p,
int  i 
) [inline]

Definition at line 71 of file rational_surface.hpp.

00071 { m_p[i]=p; }

void set_range ( Scalar  umin,
Scalar  umax,
Scalar  vmin,
Scalar  vmax 
) [inline]

Definition at line 192 of file rational_surface.hpp.

References Seq< C, R >::resize().

Referenced by rational_surface< C, N, V >::rational_surface().

00192                                                                   {
00193     m_domain.resize(0);
00194     m_domain << Point(umin,vmin) << Point(umax,vmin)
00195              << Point(umin,vmax) << Point(umax,vmin);
00196 }

C umax ( void   )  const [inline, virtual]

Implements parametric_surface< C, V >.

Definition at line 163 of file rational_surface.hpp.

References Seq< C, R >::size().

00163                      {
00164     Scalar r=m_domain[0].x();
00165     for(unsigned i=1; i<m_domain.size();i++)
00166         r=std::max(r,m_domain[i].x());
00167     return r;
00168 }

C umin ( void   )  const [inline, virtual]

Implements parametric_surface< C, V >.

Definition at line 155 of file rational_surface.hpp.

References Seq< C, R >::size().

00155                      {
00156     Scalar r=m_domain[0].x();
00157     for(unsigned i=1; i<m_domain.size();i++)
00158         r=std::min(r,m_domain[i].x());
00159     return r;
00160 }

C vmax ( void   )  const [inline, virtual]

Implements parametric_surface< C, V >.

Definition at line 179 of file rational_surface.hpp.

References Seq< C, R >::size().

00179                      {
00180     Scalar r=m_domain[0].y();
00181     for(unsigned i=1; i<m_domain.size();i++)
00182         r=std::max(r,m_domain[i].y());
00183     return r;
00184 }

C vmin ( void   )  const [inline, virtual]

Implements parametric_surface< C, V >.

Definition at line 171 of file rational_surface.hpp.

References Seq< C, R >::size().

00171                      {
00172     Scalar r=m_domain[0].y();
00173     for(unsigned i=1; i<m_domain.size();i++)
00174         r=std::min(r,m_domain[i].y());
00175     return r;
00176 }

The documentation for this class was generated from the following file:
Generated on 6 Dec 2012 for shape by  doxygen 1.6.1