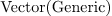| Linear factors |
1.Input and output representation
The function linear_factors computes the linear factors, with multiplicity, of a lacunary (a.k.a. super-sparse) polynomial.
The input polynomial is a sparse_polynomial<C,monomial<vector<E>
> > where C is the type of the coefficients
and E is the type of the exponents. For both, the
supported types are int and integer.
Note yet that the coefficients should be at least as large as the
exponents since this is needed to derive the polynomial. For more on
sparse_polynomial<...>, please refer to the
documentation of
The factors are returned as a vector<irreducible_factor<Sparse_polynomial>
> where Sparse_polynomial is the type of the
input. An irreducible_factor<Sparse_polynomial>
is basically a pair made of a Sparse_polynomial and
its multiplicity. For more on irreducible_factor<...>,
please refer to the documentation of
The input polynomial can be either univariate or bivariate. Depending on the dimension of the vector of variables of the input, the function linear_factors defined in linear_factors.hpp chooses to apply either linear_factors_univariate or linear_factors_bivariate.
2.Univariate polynomials
If given as input a polynomial in one variable, the function linear_factors calls linear_factors_univariate. If linear_factors_univariate is directly used, it supposes that the input polynomial has one variable. The behavior if this is not true is not guaranteed but this shall most probably result in an error.
#include <lacunaryx/linear_factors.hpp>
...
#define E integer // or int
#define C integer // or int
#define Monomial monomial< vector<E> >
#define Sparse_polynomial sparse_polynomial<C, Monomial>
...
Sparse_polynomial x (1, Monomial (vec(1))); // defines the variable x
Sparse_polynomial p= x*x*(x+1)*(x+1)*(x-2)*(x+3)*(x+3)*(x+3)*(2*x+3)*(x*x+x+1);
string s="4356768657564355757856462587657634635";
integer e(s);
p *= (1+3*binpow(x,1345) - 2*(x-4)*binpow(x,e)+(x*x*x-6)*binpow(x,2*e));
vector< irreducible_factor<Sparse_polynomial> > v= linear_factors(p);
// [(x,2),(x+1,2),(x-2,1),(x+3,3),(2*x+3,1)]
3.Bivariate polynomials
If given as input a polynomial in two variables, the function linear_factors calls linear_factors_bivariate, which in turn uses linear_factors_univariate as a subroutine. If linear_factors_bivariate is directly used, the input polynomial is supposed to be bivariate. The behavior if this is not true is not guaranteed but this shall most probably result in an error.
#include <lacunaryx/linear_factors.hpp>
...
#define E integer // or int
#define C integer // or int
#define Monomial monomial< vector<E> >
#define Sparse_polynomial sparse_polynomial<C, Monomial>
...
Sparse_polynomial x (1, Monomial (vec(1,0))); // defines the variable x
Sparse_polynomial y (1, Monomial (vec(0,1))); // defines the variable y
Sparse_polynomial p= x*x*y*(x-2)*(2*y+3)*(2*y+3)*(y-x+3)*(2*x+7*y)*(x*y+x+1);
string s="4356768657564355757856462587657634635";
integer e(s);
p *= (1 + 3*binpow(x,1345)*binpow(y,54334) - 2*(x-4*y)*binpow(x,e)*y*y + (x*x*x-6)*binpow(y,2*e));
vector< irreducible_factor<Sparse_polynomial> > v= linear_factors(p);
// [(x,2),(y,1),(x-2,1),(2*y+3,2),(y-x+3,1),(2*x+7*y,1)]
4.Use within Mathemagix
When used with univariate polynomials, the function
linear_factors can take as input a polynomial of type either
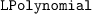or LMVPolynomial. For
multivariate polynomials, the type 
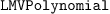has to be
used.
4.1.Univariate polynomials: LPolynomial
The function linear_factors is glued within 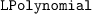(for “Lacunary Polynomial”). It is used
as follows:
Mmx]
use "lacunaryx"; type_mode? := true;
Mmx]
x : LPolynomial Integer == lpolynomial (1, 1)
: 
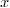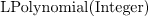
Mmx]
p : LPolynomial Integer ==
x^2*(x+1)^2*(x-2)*(x+3)^3*(2*x+3)*(x^2+x+1)
:
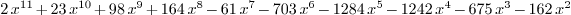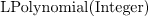
Mmx]
q : LPolynomial Integer == -x^876546523 + x^876546522 +
2*x^876546520 - 2*x^876546519 + 2*x^156476833 -
12*x^156476832 + 10*x^156476831 + 8*x^1346 - 8*x^1345 -
x + 1
:
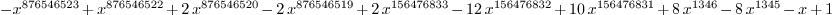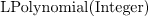
Mmx]
e : Integer == 4356768657564355757856462587657634635;
r : LPolynomial Integer == 1 + 3*x^1345 -
2*(x-4)*x^e+(x^3-6)*x^(2*e)
:
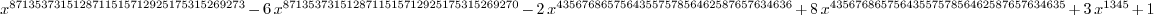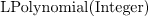
Mmx]
linear_factors (p*q*r)
: 
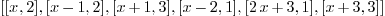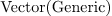
4.2.Multivariate polynomials: LMVPolynomial
The function linear_factors can also be
input a multivariate<sparse_polynomial<...>>,
as defined in
The function linear_factors is glued to
Mmx]
X : Coordinate == coordinate ('x);
x : LMVPolynomial Integer ==
lmvpolynomial(1:>Integer, X)
: 
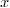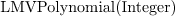
Mmx]
Y : Coordinate == coordinate ('y);
y : LMVPolynomial Integer ==
lmvpolynomial(1:>Integer, Y)
:
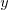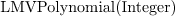
Using the mechanisms of the multivariate<...> objects, linear_factors is usable with both univariate and bivariate polynomials.
Example of use with univariate polynomials
Mmx]
p : LMVPolynomial Integer ==
x^2*(x+1)^2*(x-2)*(x+3)^3*(2*x+3)*(x^2+x+1)
:
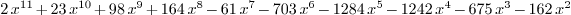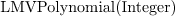
Mmx]
q : LMVPolynomial Integer == -x^876546523 + x^876546522
+ 2*x^876546520 - 2*x^876546519 + 2*x^156476833 -
12*x^156476832 + 10*x^156476831 + 8*x^1346 - 8*x^1345 -
x + 1
:
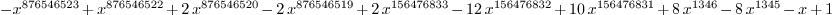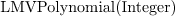
Mmx]
e : Integer == 4356768657564355757856462587657634635;
r : LMVPolynomial Integer == 1 + 3*x^1345 -
2*(x-4)*x^e+(x^3-6)*x^(2*e)
:
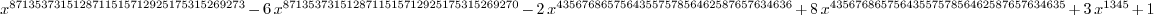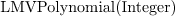
Mmx]
linear_factors(p*q*r)
:
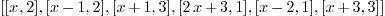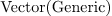
Example of use with bivariate polynomials
Mmx]
p : LMVPolynomial Integer ==
x^2*y*(x-2)*(2*y+3)^2*(y-x+3)*(2*x+7*y)*(x*y+x+1)*(3*x-6*y+5)
:
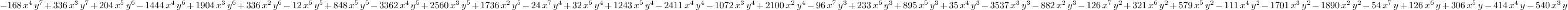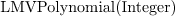
Mmx]
q : LMVPolynomial Integer == x^3*y^54354165 -
6*y^54354165 - 2*x^4*y^54354164 + 12*x*y^54354164 +
x^5*y^54354163 - 6*x^2*y^54354163 + 3*x^1345*y^54336 -
6*x^1346*y^54335 + 3*x^1347*y^54334 + 8*x^432534*y^5 -
18*x^432535*y^4 + 12*x^432536*y^3 - 2*x^432537*y^2 + y^2
- 2*x*y + x^2
:
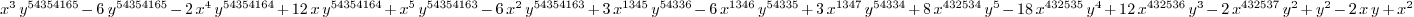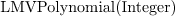
Mmx]
e : Integer == 35154014504040115230143514;
r : LMVPolynomial Integer == 1 + 3*x^1345*y^54334 -
2*(x-4*y)*x^e*y^2 + (x^3-6)*y^(2*e)
:
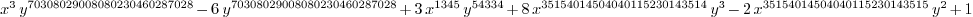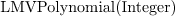
Mmx]
linear_factors (p*q*r)
:
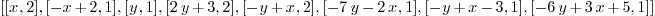