| Integer roots |
1.Function integer_roots
The function integer_roots computes the integer roots, with multiplicity, of a lacunary (a.k.a. super-sparse) polynomial. This function is implemented in the file integer_roots.hpp.
The input polynomial is a sparse_polynomial<C,monomial<vector<E>
> > where C is the type of the coefficients
and E is the type of the exponents. For both, the
supported types are int and integer.
Note yet that the coefficients should be at least as large as the
exponents since this is needed to derive the polynomial. For more on
sparse_polynomial<...>, please refer to the
documentation of
The roots are returned as a vector< pair<C,E> > where in each pair<C,E> the first component is the root and the second is its multiplicity.
#include <lacunaryx/integer_roots.hpp>
...
#define E integer // or int
#define C integer // or int
#define Monomial monomial< vector<E> >
#define Sparse_polynomial sparse_polynomial<C, Monomial>
...
Sparse_polynomial x (1, Monomial (vec(1))); // defines the variable x
Sparse_polynomial p= x*x*(x+1)*(x+1)*(x-2)*(x+3)*(x+3)*(x+3)*(2*x+3)*(x*x+x+1);
string s="4356768657564355757856462587657634635";
integer e(s);
p *= (1+3*binpow(x,1345) - 2*(x-4)*binpow(x,e)+(x*x*x-6)*binpow(x,2*e));
vector< pair<C,E> > v= integer_roots(p); // [(0,2),(-1,2),(2,1),(-3,3)]
2.Use within Mathemagix
2.1.Lacunary polynomials
The lacunaryx package comes with a new type for polynomials
called LPolynomials. The function integer_roots
is glued within
Mmx]
use "lacunaryx"; type_mode? := true;
Mmx]
x : LPolynomial Integer == lpolynomial(1:> Integer,
1)
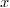 :
: 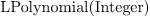
Mmx]
p : LPolynomial Integer ==
x^2*(x+1)^2*(x-2)*(x+3)^3*(2*x+3)*(x^2+x+1)
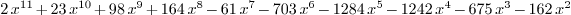 :
: 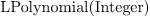
Mmx]
q : LPolynomial Integer == -x^876546523 + x^876546522 +
2*x^876546520 - 2*x^876546519 + 2*x^156476833 -
12*x^156476832 + 10*x^156476831 + 8*x^1346 - 8*x^1345 -
x + 1
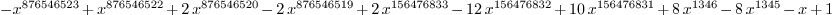 :
: 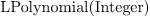
Mmx]
roots (p*q)
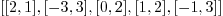 :
: 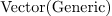
2.2.Multivariate polynomials
The function integer_roots can also take
as input a multivariate<sparse_polynomial<...>>,
as defined in
The function integer_root is glued to
Mmx]
X : Coordinate == coordinate ('x)
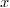 :
: 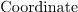
Mmx]
x : LMVPolynomial Integer ==
lmvpolynomial(1:>Integer, X)
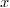 :
: 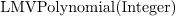
Mmx]
p : LMVPolynomial Integer ==
x^2*(x+1)^2*(x-2)*(x+3)^3*(2*x+3)*(x^2+x+1)
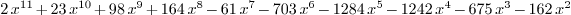 :
: 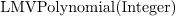
Mmx]
q : LMVPolynomial Integer == -x^876546523 + x^876546522
+ 2*x^876546520 - 2*x^876546519 + 2*x^156476833 -
12*x^156476832 + 10*x^156476831 + 8*x^1346 - 8*x^1345 -
x + 1
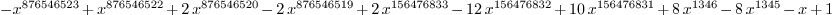 :
: 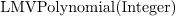
Mmx]
roots(p*q)
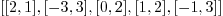 :
: