|
|
JORIS VAN DER HOEVEN, GRÉGOIRE
LECERF, BERNARD MOURRAIN, PHILIPPE TRÉBUCHET,
JÉRÉMY BERTHOMIEU, DAOUDA NIANG
DIATTA, AND ANGELOS MANTZAFLARIS
|
|
|
Abstract. We describe the goals and
architecture of the software project Mathemagix,
the main list of packages it contains, the main characteristics of its
programming language, and connections with existing front-ends.
1.Context and objectives
Symbolic computation is usually associated with computer algebra systems
such as Axiom, Maple Mathematica, Magma, etc which
provide large communities of users with several high level mathematical
functionalities. Although these software are equipped with high level
programming languages, their interpreters may suffer from efficiency
when it comes to dedicated and optimized low level computations. In
addition, commercial software do not allow the user to freely inspect
and modify the source code for experimenting new low level algorithms.
On the other hand several special purpose C/C++ libraries, such as
Gmp, Mpfr, Pari/GP,
Ntl, Macaulay, Singular,
Cocoa, Fgb, Lapack,
etc, have been developed, and have now become increasingly powerful for
solving the tasks they were designed for. Nevertheless, using several of
them together in a single application often requires advanced
programming skills.
In the recent years, appeared general purpose open source software such
as Maxima, Axiom, Octave, Scilab, Sage,
etc featuring an easier integration of different specialized packages
with a unified open source framework, such as Python
used in Sage. Another approach to tackle the
efficiency problem while implementing easily new functionalities,
adopted by Aldor, is to design a compiler for a
language well suited to scientific programming, and which leads to
efficient standalone executables. Our goals within the development of
Mathemagix are in these two mainstreams, without
compromising modularity for efficiency or vise-versa. In particular, we
wish:
-
to provide a coherent open source framework for the development and
publication of efficient and stand-alone packages;
-
to provide packages, which implement in a very efficient way the
elementary operations needed in algebraic and numeric computation;
-
to provide tools for the connection of these packages to other
interpreters, in particular to the Mathemagix
interpreter;
-
to provide a high-level programming language, adapted to
mathematical computation, along with both an interpreter and a
compiler for that language;
-
to provide high level user interfaces, based on external tools such
as TeXmacs (available from http://www.texmacs.org)
for a graphical front-end with high quality typesetting for
mathematical formulas and Axel for 3D
algebraic modeling (available from http://axel.inria.fr).
2.Distribution
Mathemagix is freely distributed mainly under the GPL license. It can be
downloaded from http://www.mathemagix.org. Automatic
configuration and building is ensured via either the GNU
Autotools or Cmake. At the present time
only Mac OS X and Linux platforms are supported.
To achieve modularity and scalability, Mathemagix
is organized as a collection of packages with dag-like dependencies.
Each of them provides a C++ interface for gluing
some of its functionalities to the Mathemagix
interpreter. It can also provide code written in the Mathemagix
language, or gluing code for the interaction with other applications
such as Axel.
To generate automatically the glue for the interpreter, the tool autoglue (also written in the Mathemagix
language) can be used. It takes the Mathemagix
files (.mmx) as input and produces the corresponding
C++ files (.cpp) for the glue. A
Mathemagix glue file contains a dictionary between
the functions imported in the interpreter, described by their
signatures, and the corresponding C++ functions.
Signatures with type parameters (that are templates in C++)
are allowed. The gluing C++ code of a function is
generated if all the types involved in its signature are specialized
(using the keyword specialize). The generated C++ files
can then be compiled and assembled into a dynamic library.
3.Packages
Most of the packages are written in C++, the remaining code is written
in the Mathemagix language. The current list of
packages represents about 400,000 effective lines of code. This list of
packages is in constant evolution. We list here the main ones:
-
basix
-
This package contains the basics, that is data structures for
symbols, lists, arrays, hash tables, etc. It also provides a
system for generic objects. Parsers and pretty printers, together
with a system for keeping track of locations in the source code
and generating error messages are also available. Important
operators for systematic use throughout the project and the glue
facility, both for interpreters and functionality can also be
found in this package.
-
numerix
-
It provides a C++ interface for extended arithmetic over integers,
over rational numbers based on Gmp, and over
floating point numbers based on Mpfr.
Complexified version of these types are also provided as well as
intervals and balls for certified arithmetic. Modular numbers are
also implemented herein.
-
algebramix
-
This package aims to provide basic routines on univariate
polynomials, series, 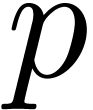 -adic
numbers and matrices with state-of-the-art asymptotic time
complexities.
-adic
numbers and matrices with state-of-the-art asymptotic time
complexities.
-
multimix
-
This package is dedicated to transseries and optimized computation
on dense and sparse multivariate polynomials and series.
-
analyziz
-
This package contains tools for effective analytic computation,
including analytic continuation and manipulation of effective
analytic functions.
-
linalg
-
This package provides basic linear algebra tools on dense
matrices, with any suitable coefficients (float,
double, long double, extended
precision, and modular arithmetic where it makes sense). Its
interface is fully compliant with the standard Blas
and Lapack libraries one, allowing us to
transparently use a specialized implementation such as Atlas for usual machine type coefficients.
-
newmac
-
The main tool provided by this package is a multivariate
polynomial system solver, which uses the well known border bases
technique for solving polynomial systems. It can compute a
representation of the quotient algebra, and when the input system
admit only finitely many solution, it can output numerical
approximations of the roots, and a certificate for the precision
of the root approximations.
-
realroot
-
Subdivision solvers for univariate polynomials using Bernstein or
monomial basis representation are implemented here. This package
also includes a very efficient univariate solver, which computes
the continued fraction expansion of the real roots of a
polynomial. Subdivision solvers for multivariate polynomials using
Bernstein basis representation, sleeve approximation and
preconditioner are also available in this package.
-
polytopix
-
In this package, tools for the manipulation of polytopes
(represented by inequalities or by generators) and connection with
multivariate polynomial supports are available. The polytope
manipulations are based on the Cdd library.
A plugin for Axel is also available.
-
shape
-
This package provides data structures to manipulate algebraic
curves and surfaces which are given by equations or by
parameterizations. It also contains tools to compute, in a
certified way, the topology of algebraic sets, arrangements,
(self-)intersection curves of parameterized surfaces,
singularities…
Other packages are still in development, for finite fields, symbolic
expressions, asymptotic analysis, numeric homotopy continuation for
polynomial system solving, and polynomial factorization.
4.Towards a new high level language
The aim of the Mathemagix language is to provide a
new high level language, with the following characteristics:
-
Strong typedness
-
It is strongly typed, with support for overloading, implicit
conversions, generic objects, compile-time type checking and,
possibly, built-in support for expression types which interact
with the type system.
-
High level control structures
-
High level control structures, like coroutines, generators,
exceptions, continuations, etc.
-
Reusability of external libraries
-
Besides achieving runtime efficiency of Mathemagix
itself, the aim is to achieve runtime efficiency through the
extensive reuse of existing dedicated libraries written in other
languages. Mathemagix therefore implements
transparent mechanisms for reusing external libraries and in
particular C++ template libraries.
Currently, a rather slow interpreter of only a part of the full
language, the mmxlight package, is provided. A compiler
and a new faster interpreter, written in the Mathemagix
language, are under development in the mmcompiler
package.
5.Front-ends
-
A textual shell mode
-
Mathemagix provides the user with a usual
ASCII shell mode and a convenient advanced programmer interface,
based on a dedicated Emacs mode.
-
A graphical interface
-
It can be used within GNU TeXmacs as a primary graphical
interface. This offers a unified and user friendly framework for
editing structured documents with different types of content
(text, graphics, mathematics, etc.), including
interactive content such as Mathemagix
sessions. The rendering engine uses high-quality typesetting
algorithms so as to produce professionally looking documents,
which can either be printed out or presented from a laptop. It is
also used to write and to generate the top-level documentation of
the packages in different format (html, tex),
in combination with Doxygen for the C++ code documentation.
-
A geometric modeler
-
The program is connected to the algebraic-geometric modeler Axel as a tool for visualisation
and geometric computation. Currently some packages of Mathemagix are directly used to build the
computational kernel of Axel (realroot,
shape). Other packages (eg. polytopix)
produce independent plugins, which extend the interface and the
functionalities of the algebraic-geometric modeler. The connection
between the interpreter Mmxlight and Axel is under development, in order to get a
bidirectional interoperability of the two applications.
6.Example of asymptotic expansions within
TeXmacs front-end
Mmx] |
x == infinity ('x); 1 / (1 + x + exp x) |
| Mmx] |
product (x + log x, x) asymptotic expansion of 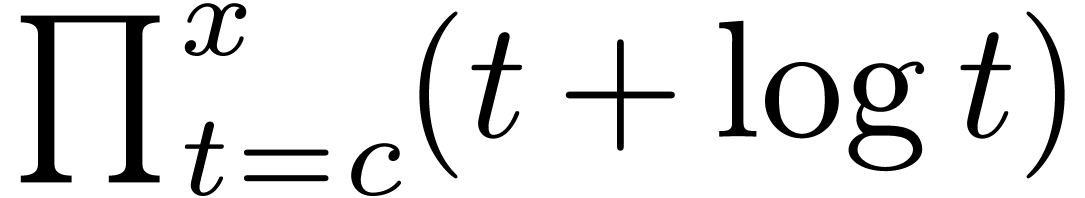 for for  |
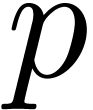 -adic
numbers and matrices with state-of-the-art asymptotic time
complexities.
-adic
numbers and matrices with state-of-the-art asymptotic time
complexities.
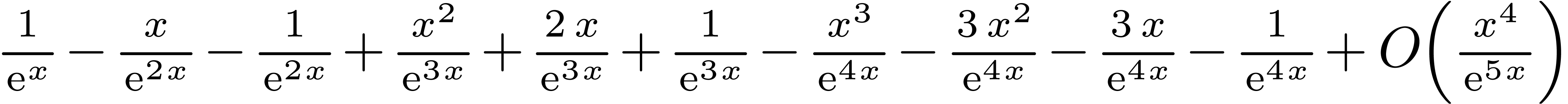
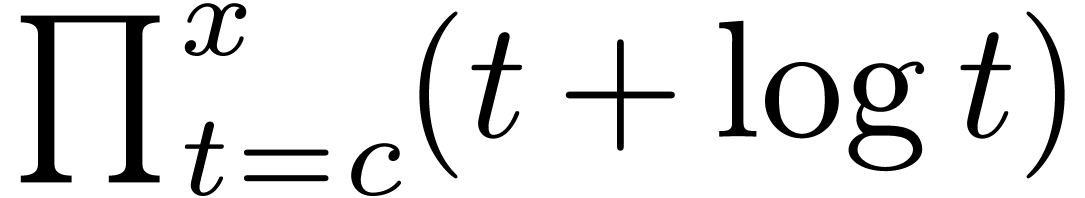 for
for