Presentation of the algorithm

The geometric resolution algorithm is a Gröbner-free alternative for solving polynomial systems of equations and inequations. It computes a lifting fiber of the system (see e.g. [Giusti, Lecerf, Salvy - A Gröbner free alternative for polynomial system solving]).

Its current implementation in Mathemagix handles only certain polynomial systems in input, that are systems of equations that form a regular reduced sequence. This restriction implies in particular that there are the same number of equations and variables and that the solutions of the system are a set of points.

Lifting step

The geometric resolution algorithm is based on three steps which are repeated as many times as there are variables: a lifting step, an intersection step and a cleaning step.

A new feature is that a relaxed variant of the lifting step is implemented for the first time. It uses the recursive power series and 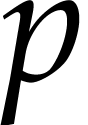-adic integers framework of the algebramix package.

The default lifting variant is called with the implementation variant V=lifting_fiber_naive of the type lifting_fiber<C,V>. The relaxed variant is obtained with the variant lifting_fiber_relaxed<V>.

Use from the interpreter

Mmx]  

use "geomsolvex"

Mmx]  

X == coordinate ('x); Y == coordinate ('y);

Mmx]  

x == polynomial_dag (1 :> Rational, X);
y == polynomial_dag (1 :> Rational, Y);

Mmx]  

f1 == x^2 + y^2 - 1;
f2 == x^2 + x * y - 2;

Mmx]  

geometric_solve_reduced_regular% ([f1, f2])

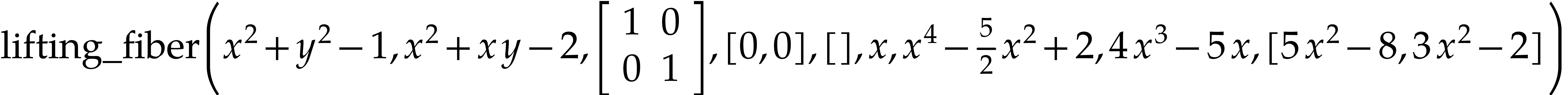
Let us explain roughly what a lifting fiber is on this example. It starts with a linear change of variable

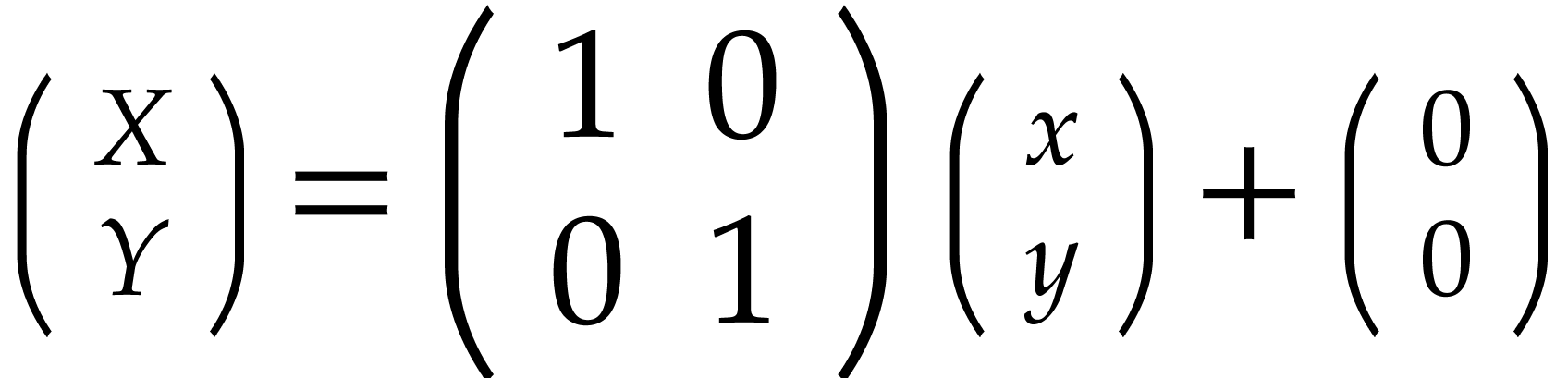
which is trivial in this case. Then we have a minimal polynomial 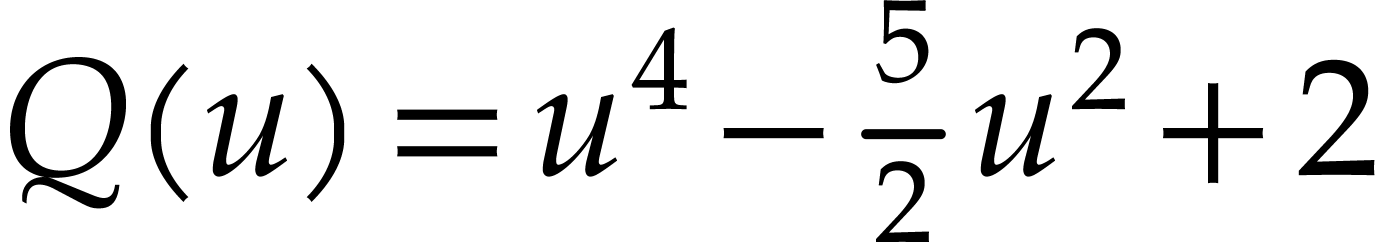and parametrizations (one per variable)

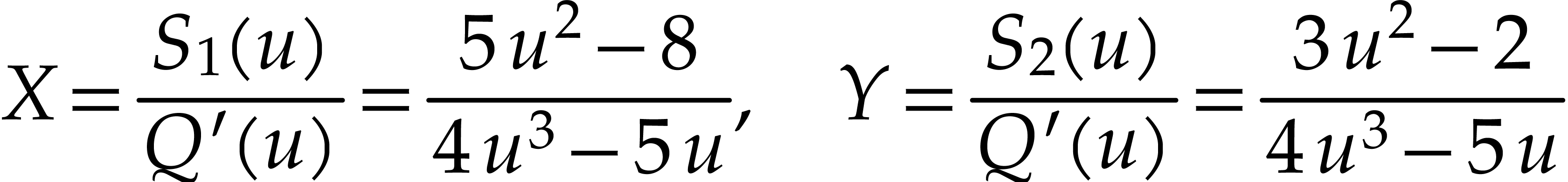
over a common denominator 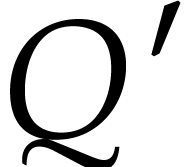. These parametrizations satisfy the input system

Mmx]  

p: Integer == 101;

Mmx]  

x == polynomial_dag (1 :> Integer, X);
y == polynomial_dag (1 :> Integer, Y);

Mmx]  

f1 == x^2 + y^2 - 1;
f2 == x^2 + x * y - 2;

Mmx]  

geometric_solve_reduced_regular% ([f1 mod p, f2 mod p])

For long computations, verbosity can be enabled by setting geomsolvex_verbose.