Several important template classes, such as vector, matrix, polynomial and series admit a last template parameter V, called the implementation variant (or the traits class, in C++ terminology). For most 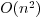Mathemagix template classes, the class itself determines the internal representation of instances. For instance, the polynomial class corresponds to dense univariate polynomials, determined by a low level vector of coefficients. The implementation variant is used to specify the actual algorithms which are used for common operations. For instance, the polynomial_naive variant uses the naive algorithm for polynomial multiplication, whereas Karatsuba multiplication is used by the variant polynomial_karatsuba<polynomial_naive>.

As is suggested by the variant polynomial_karatsuba<polynomial_naive>, new variants can be built on top of other variants and existing variants can be customized. Typically, an implementation of dense polynomials provides several features:

• Vectorial routines on polynomials, such as addition.

• Other linear-time routines, such as differentiation.

• Multiplication.

• Division.

• Greatest common divisor.

• Several higher level routines, such as subresultants or multi-point evaluation.

Variants and features are essentially empty classes, which are mainly used as template parameters. Mathemagix provides a standard implementation helper class, which allows to associate a concrete implementation to a feature and variant.

For instance, polynomial multiplication corresponds to the feature polynomial_multiply. The main multiplication routine for dense polynomials is a static member function

implementation<polynomial_multiply,polynomial_naive>::mul

of the implementation helper class. This routine directly operates on vectors in memory:

template<typename C, typename K> static void
mul (C* dest, const C* s1, const K* s2, nat n1, nat n2) {
  if (n1+n2>0)
    Pol::clear (dest, n1+n2-1);
  while (n2 != 0) {
    Pol::mul_add (dest, s1, *s2, n1);
    dest++; s2++; n2--;
  }
}

Here Pol is an alias for implementation<polynomial_linear,polynomial_naive>, hence the implementation of naive multiplication relies on the implementation of naive vectorial and linear-time algorithms on polynomials.

From the high level point of view, the implementation of polynomial multiplication for the type polynomial<C,V> relies on the low level multiplication algorithm determined by the variant V:

template<typename C, typename V> polynomial<C,V>
operator * (const polynomial<C,V>& P1, const polynomial<C,V>& P2) {
  typedef implementation<polynomial_multiply,V> Pol;
  nat n1= N(P1), n2= N(P2);
  if (n1 == 0 || n2 == 0) return polynomial<C,V> ();
  nat l= aligned_size<C,V> (n1+n2-1);
  C* r= mmx_new<C> (l);
  Pol::mul (r, seg (P1), seg (P2), n1, n2);
  return polynomial<C,V> (r, n1+n2-1, l);
}

A default variant is usually defined in terms of the remaining template parameters. In the case of polynomials, this is accomplished by means of the polynomial_variant_helper template: for any coefficient type C, polynomial_variant_helper<C>::PV yields the default variant for C.

In fact, the template implementation takes three arguments: the feature, the polynomial variant and the variant for the actual implementation. This allows for the customization of a specific feature. More precisely, assume that we are given a feature F and a variant V and that we want to define a new variant customized<V> with a different implementation of the feature F, but unaltered implementations of all other features. This is achieved using a code of the type

template<typename V, typename W>
struct implementation<F,V,customized<W> >:
  public implementation<F,V,W>
{
  typedef implementation<F,V,W> Fallback;
  ...
};

For the actual implementation of the customized feature, one may rely on the original implementation Fallback specified by the variants V and W. Here we notice that implementation<F,V> is equivalent to implementation<F,V,V>.

We recall that the variant mechanism is only used in order to implement different algorithms for a similar functionality, while presupposing a given internal representation. Some higher level functions on polynomials may still be correct for polynomials with alternative internal representations. In that case, a new template class should be defined for each alternative representation, such as sparse_polynomial. This class should be implemented with care, so as to match the same signature as the usual dense class polynomial. For instance, if we have an operation

template<typename C, typename V> polynomial<C,V>
foo (const polynomial<C,V>& p) { ... }

which is not specific to dense polynomials, then we should have its sparse counterpart with the same name

template<typename C, typename V> sparse_polynomial<C,V>
foo (const sparse_polynomial<C,V>& p) { ... }

The high level functionality bar can then be implemented by using the class of polynomials itself as a template parameter:

template<typename Pol> Pol
bar (const Pol& p) {
  return foo (foo (p));
}