| Power series |
1.Introduction
Power series are implemented within the class series from series.hpp.
#include <numerix/rational.hpp>
#include <algebramix/series.hpp>
series<rational> z (rational (1), 1); // variable z
series<rational> f = 1 / (1 - z);
mmout << f[10] << "\n";
Series are implemented in a lazy way, which means that the precision has not to be specified in advance. Computations are actually done when a coefficient is actually needed.
The precision used for printing the power series can be set to n in the following way:
series<C,V>::set_output_order (n);
Instead of printing an approximation of the series, it is possible to display the formula it has been built from, as follows:
series<C,V>::set_formula_output (true);
Withing equality test the precision to be taken into account can be set to n via:
series<C,V>::set_cancel_order (n);
The name of the variable to be printed can be set to z with the following command:
series<C,V>::set_variable_name ("z");
2.Naive algorithms
Naive algorithms for power series are implemented in series_naive.hpp. For instance the product implemented therein has a quadratic cost.
Over numerical types, elementary functions are available from series_elementary.hpp.
3.Relaxed algorithm
The relaxed product for power series is implemented in series_relaxed.hpp.
#include <numerix/rational.hpp>
#include <algebramix/series.hpp>
#include <algebramix/series_relaxed.hpp>
#define V series_relaxed<series_naive>
series<rational,V> z (rational (1), 1); // variable z
series<rational,V> f = 1 / (1 - z);
mmout << z[10] << "\n";
The relaxed product has a softly linear cost.
4.Recursive series
A series 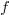 is said to be recursive if it
satisfies an equation
is said to be recursive if it
satisfies an equation 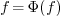 that allows to compute
the
that allows to compute
the 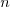 -th coefficient of
-th coefficient of 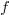 as the
as the 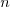 -th coefficient of
-th coefficient of 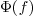 with the only knownledge of the
with the only knownledge of the  first
coefficients of
first
coefficients of 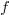 , whenever
, whenever 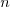 is larger than an integer
is larger than an integer 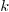 called the
index.
called the
index.
For example 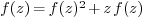 +1, with
+1, with 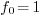 can be implemented as follows:
can be implemented as follows:
template<typename C, typename V>
struct example_series_rep : recursive_series_rep<C,V>
example_series_rep () {}
syntactic expression (const syntactic& z) const {
return apply ("example", z); }
series<C,V> initialize () {
series<C,V> f= this->me ();
this->initial (0)= C(1);
return square (f) + lshiftz (f, 1) + C(1); }
template<typename C, typename V>
example_series () {
series_rep<C,V>* rep= new example_series_rep<C,V> ();
return recursive (series<C,V> (rep)); }
5.Implicit series
Implicit series are implemented in series_implicit.hpp.
6.Vectorial operations
Vectorial and matricial auxilary functions are available from series_vector.hpp and series_matrix.hpp respectively. They are useful for computing recursive vectors of series.
7.Mathemagix
interface
Mmx]
use "algebramix";
type_mode? := true;
Mmx]
z == series (0 :> Rational, 1 :> Rational)
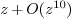 :
: 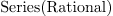
Mmx]
f == log (1 - z)
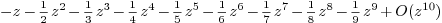 :
: 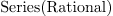
Mmx]
f[20]
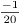 :
: