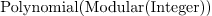| Univariate polynomials |
1.Naive algorithms
Univariate polynomials over C are implemented in the class polynomial<C,V>, defined in polynomial.hpp. The default variant polynomial_naive assumes that C is a field, not necessarily commutative. This provides implementations of the naive algorithms. For instance the product, the division, and the gcd have quadratic costs.
#include <numerix/rational.hpp>
#include <algebramix/polynomial.hpp>
...
polynomial<rational> x (C(1), 1); // defines the monomial x
polynomial<rational> p= square (x) + 3 * x + 1;
Remark that you cannot use the infix operation ^ for
powering, for it is usually reserved to bitwise operations. Instead
you can use binary powering with binpow (a, n). For
the sake of efficiency, the monomial 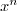 must be
constructed as polynomial<C,V> (C(1), n).
must be
constructed as polynomial<C,V> (C(1), n).
For polynomials over a ring you must add the variant poynomial_ring_naive<V> defined in polynomial_ring_naive.hpp, that essentially contains
implementations for the subresultants due to
2.Divide and conquer algorithms
All classical generic divide and conquer algorithms over any field are
implemented in polynomial_dicho.hpp.
Therein is defined the variant polynomial_dicho<V>
that implements the Karatsuba product, division with Newton's
inversion algorithm, fast Euclidean sequence, the half-gcd algorithm,
Padé approximants, fast multipoint evaluation and
interpolation, fast multimod and Chinese remaindering. If you want
these algorithms to be applied in 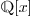 you can
modify the above piece of code into:
you can
modify the above piece of code into:
#include <algebramix/polynomial.hpp>
#include <algebramix/polynomial_dicho.hpp>
#define polynomial_dicho<polynomial_naive> V
...
polynomial<rational,V> x (C(1), 1); // defines the monomial x
polynomial<rational,V> p= square (x) + 3 * x + 1;
For polynomials over a ring you must add the variant polynomial_ring_dicho<V> defined in polynomial_ring_dicho.hpp, that essentially contains the half-subresultant alsgorithm.
3.Asymptotically fast algorithms
Schönhage & Strassen's, and Cantor & Kaltofen's fast products are implemented in polynomial_schonhage. It supports any ring with unity. This provides the generic a default variant.
4.Special types of coefficients
4.1.Kronecker's subtitution
The Kronecker susbstitution is available for polynomials over polynomials, hardware or long integers, and also with modular coefficients. One must include one of the corresponding files:
4.2.Modulars
If the coefficient ring are modular numbers then a special product is available from polynomial_modular.hpp: it first computes the product of the polynomials made of the preimages of the coefficients and reduces the coefficients at the end.
4.3.Complex numbers
For polynomial over complex numbers you must use polynomial_complex.hpp.
4.4.Quotient fields
If coefficients are in a quotient field of type quotient, then one should include polynomial_quotient.hpp. A special variant is directly available for rational numbers in polynomial_rational.hpp.
5.Quotient ring
Operations in 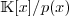 are available through the class
modular. Special types of moduli for polynomials is
defined in modular_polynomial.hpp.
are available through the class
modular. Special types of moduli for polynomials is
defined in modular_polynomial.hpp.
#include "numerix/rational.hpp"
#include "algebramix/modular_polynomial.hpp"
#define C rational
#define Polynomial polynomial<C>
#define Modular modular<modulus<Polynomial> >
...
Polynomial x (C(1), 1);
Polynomial p= square (x) - 2;
Modular::set_modulus (p);
mmout << binpow (Modular (x), 1000) << "\n";
6.Mathemagix
interface
Mmx]
use "algebramix";
type_mode? := true;
Mmx]
x == polynomial (0, 1)
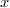 :
: 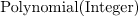
Mmx]
(1 + x)^5
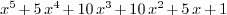 :
: 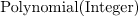
Mmx]
gcd (1 + 2*x + x^2, 1 - x^2)
 :
: 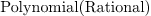
Mmx]
discriminant (1 + x + x^2)
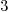 :
: 
Mmx]
(1 + x)^5 mod 5
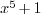 :
: