Naive algorithms for bidirectional multi-modular transformers are implemented in crt_naive.hpp.

The following piece of code computes 101 modulo 2, 3, 5, and 7:

#include "crt_int.hpp"
...
crt_naive_transformer<int> crter (vec (2, 3, 5, 7));
mmout << direct_crt (101, crter) << "\n";

Here crt_int.hpp contains specific routines for hardware integers.

1.Coverings

Let 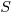be a subset of a ring 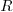. A covering 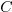of 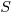is a set of coprime elements of 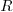such that any element of 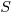is uniquely charaterized by its residues modulo all the elements of .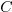

The class moduli_helper<C,Modulus> provides the user with a default covering in a specific size whose definition actually depends on 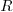. For example for the integers, the following instructions fill the vector 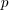with a covering for integers of 30 bits.

vector<modulus<int> > p;
bool t= moduli_helper<int, modulus<int> >::covering (p, 30);

Here the default covering being used is made of the sequence of the prime numbers: 2, 3, 5, 7, 11, etc. The value returned in t is false if no covering can be made for the specified size. Otherwise true is returned.

The sequence used for the covering can be specified as an extra argument:

#define Seq fft_prime_sequence_int<10>
vector<modulus<int> > p;
bool t= moduli_helper<int, modulus<int>, Seq>::covering (p, 30);

Here are used prime numbers of at most 10 bits. The first ones are well-suited to FFT.

Support for long integers is available in crt_integer.hpp. The following piece of code covers signed integers of 1000 bits with prime hardware integers of at most 20 bits:

#include <algebramix/crt_integer.hpp>
#define Seq fft_prime_sequence_int<20>
vector<modulus<int, modulus_int_preinverse<20> > > p;
bool t= moduli_helper<int, modulus<int>, Seq>::covering (p, 1000);

2.Transformers

The divide and conquer algorithm is implemented in crt_dicho.hpp:

#include <algebramix/crt_integer.hpp>
// let p be a covering obtained as described above
crt_dicho_transformer<integer> crter (p);

If the moduli are small, it is often faster to use the naive algorithm. While for large moduli the divide and conquer has soft linear cost. In crt_blocks.hpp is implemented a class to stack two different kinds of transformers in the following way:

#define Crter_naive crt_naive_transformer<integer, modulus<int> >
#define Crter_dicho crt_dicho_transformer<integer>
#define Crter crt_blocks_transformer<Crter_naive, Crter_dicho, 10>

Here 10 is the threshold between the two transformers: each block of 10 moduli is using the naive algorithm, and then the dichotomic algorithm is called with the moduli obtained from the products of those of each block.