| The |
Formalization of the Mathemagix
language
Let us start with formalizing the part of the  of constant symbols. Expanding
of constant symbols. Expanding  by the constant symbols
by the constant symbols 
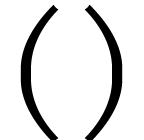 ,
,  and the function symbols
and the function symbols
 ,
,  ,
,  and
and  , we obtain the set of terms
, we obtain the set of terms  . More precisely,
. More precisely,  is the smallest
set which contains
is the smallest
set which contains  and such that:
and such that:
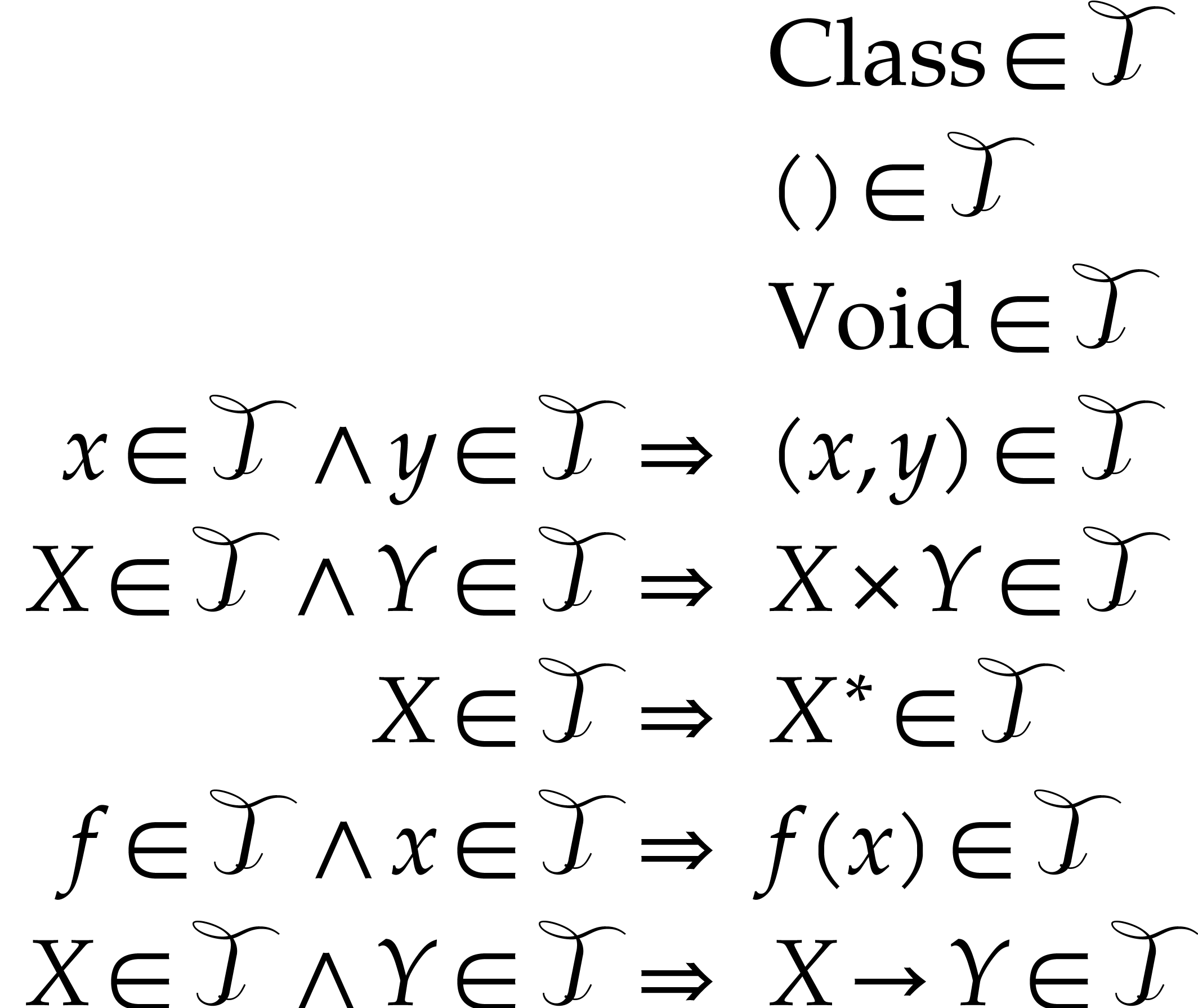
 ” and
” and  will
be assumed to be binary operators with neutral elements
will
be assumed to be binary operators with neutral elements 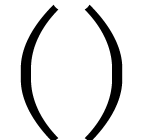 and
and  . For instance
. For instance 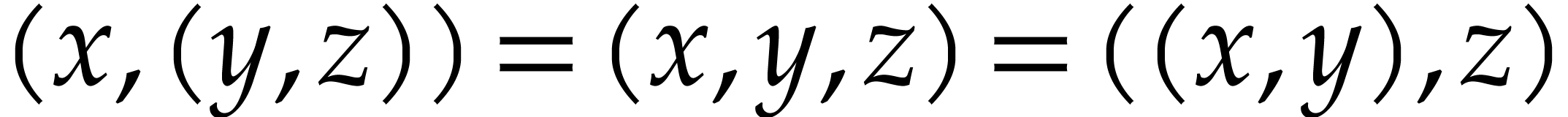 and
and 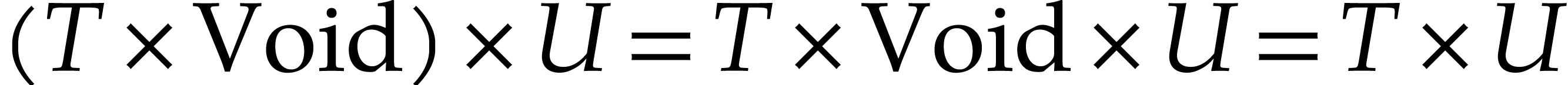 . Using the operators
“,” and
. Using the operators
“,” and 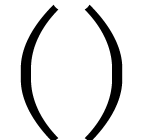 , we can thus form
, we can thus form  -ary tuples. In combination with the primitive for
function application, we can thus form
-ary tuples. In combination with the primitive for
function application, we can thus form  -ary
function applications, even though
-ary
function applications, even though  only
contains constant symbols.
only
contains constant symbols.
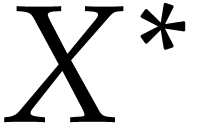 will be used for the tuple type, which is
recursively defined by
will be used for the tuple type, which is
recursively defined by  .
.
Expanding  with the binary relation
with the binary relation  and the usual logical connectors and quantifiers, we
obtain the set
and the usual logical connectors and quantifiers, we
obtain the set  of formulas. More precisely,
of formulas. More precisely,
 is the smallest set such that
is the smallest set such that
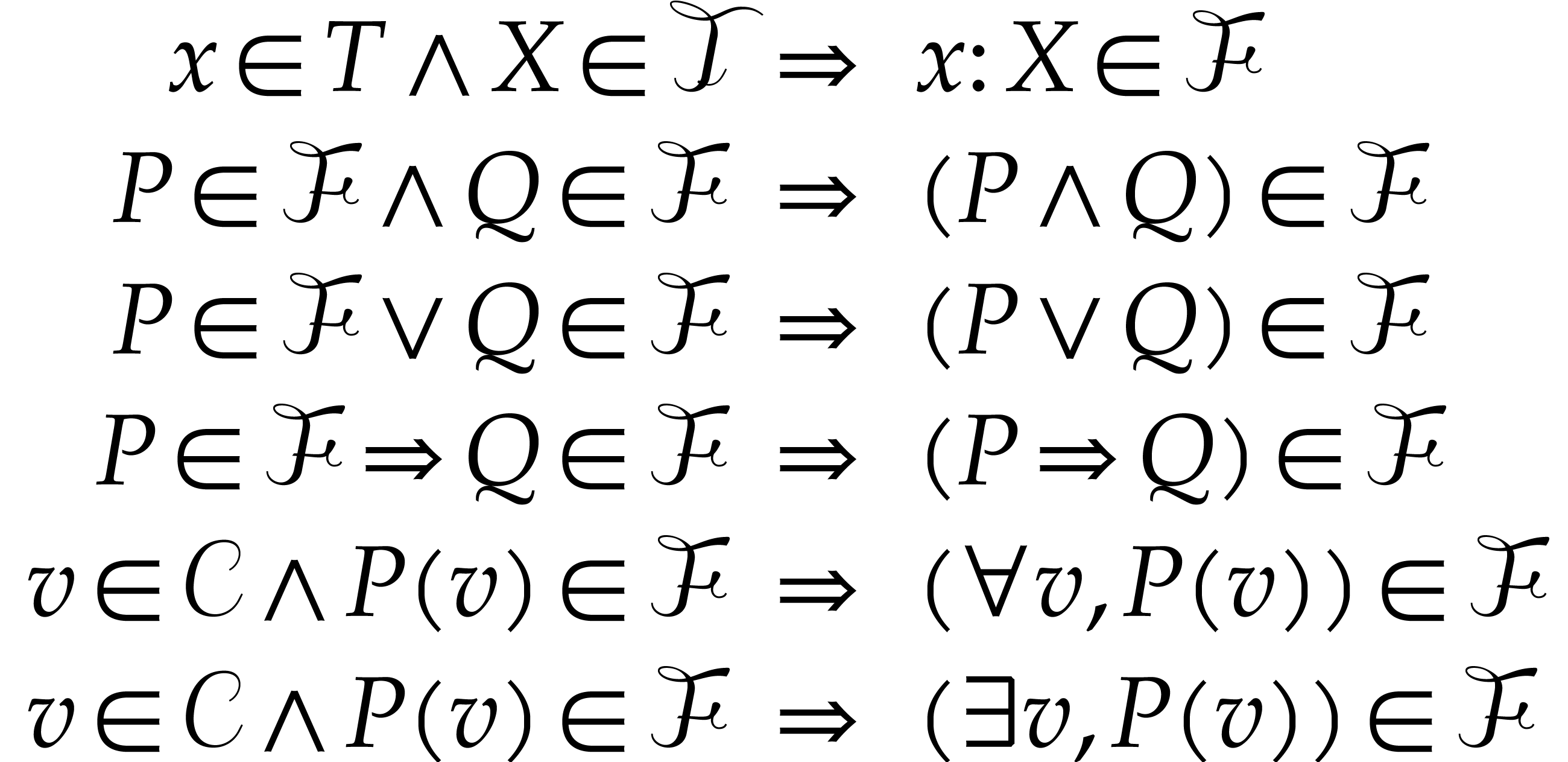
In the case of the expressions 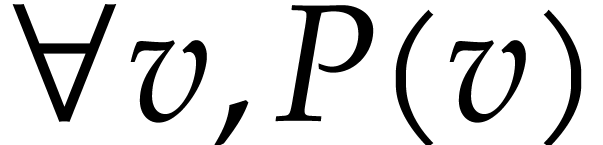 and
and  we will always assume that
we will always assume that  ,
whenever
,
whenever 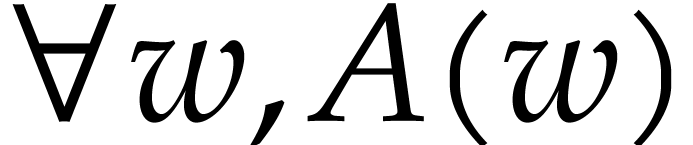 or
or  is a
subexpression of
is a
subexpression of 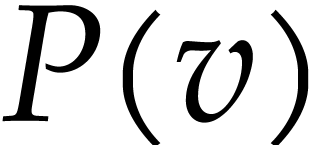 . We will also use
. We will also use 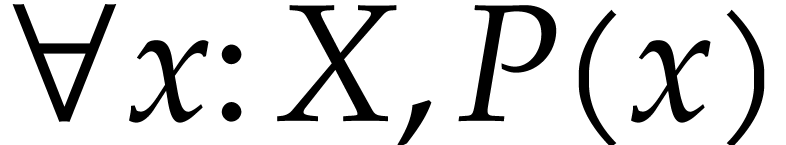 and
and 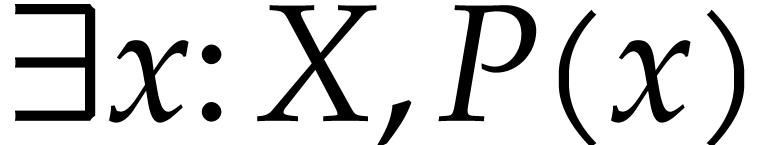 as abbreviations for
as abbreviations for 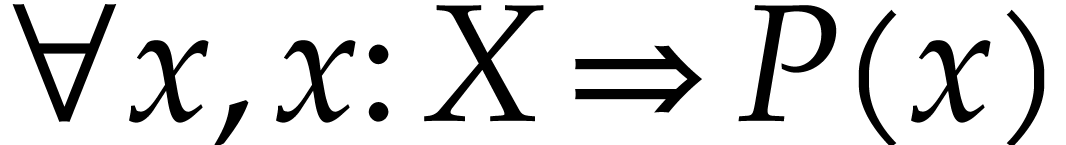 and
and 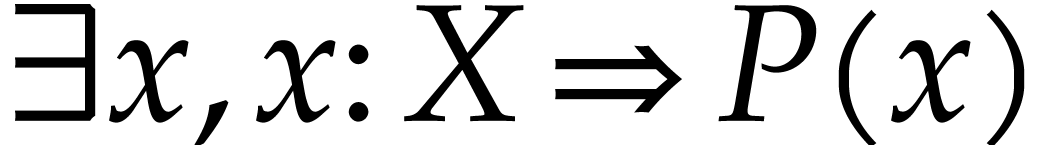 .
.
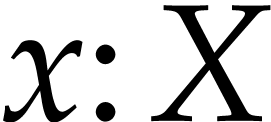 should be read “
should be read “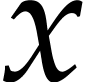 admits an interpretation of type
admits an interpretation of type 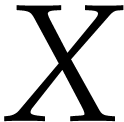 ”.
Indeed,
”.
Indeed, 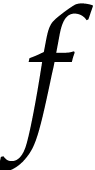 is an overloaded function,
then we may for instance both have
is an overloaded function,
then we may for instance both have  and
and 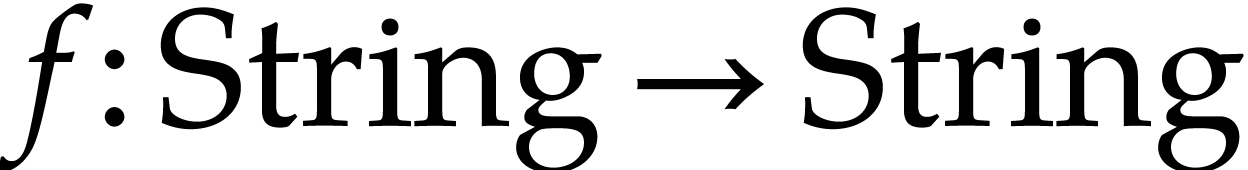 . Similarly, in presence of an
automatic converter
. Similarly, in presence of an
automatic converter 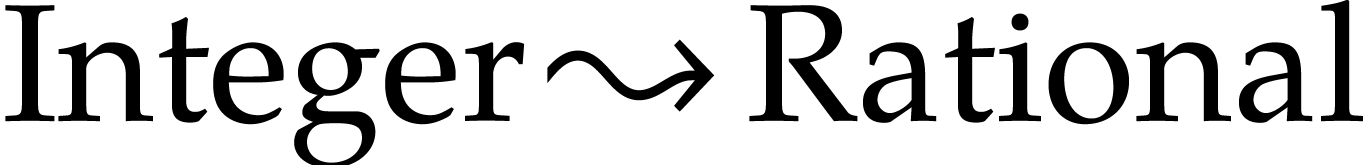 , the relation
, the relation  will automatically imply
will automatically imply  .
.
The formal theory for Mathemagix
The formal theory for the
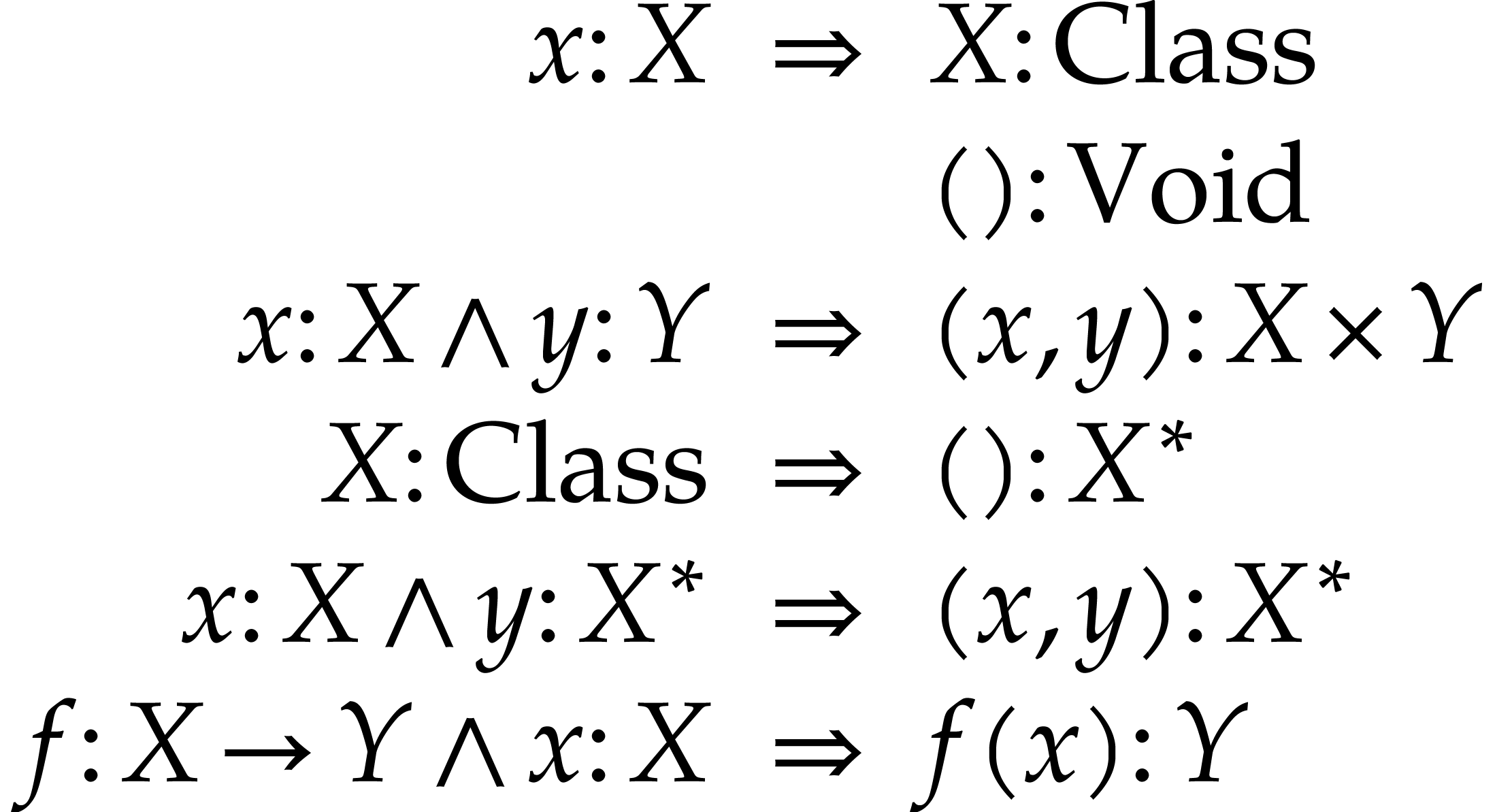
We recall our conventions concerning “,” and  , which can be restated as axioms:
, which can be restated as axioms:
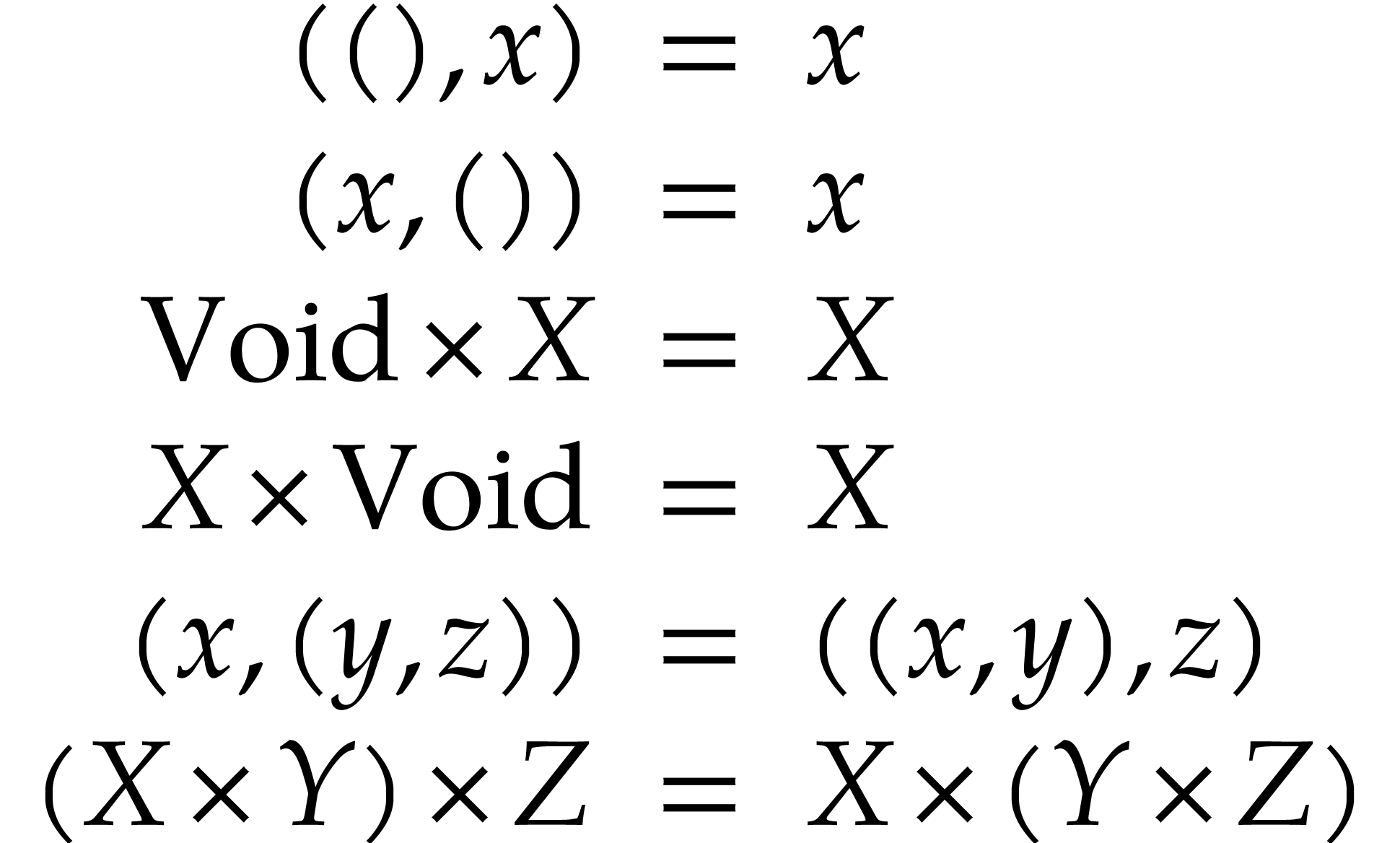
It will convenient to define the relation  by
by
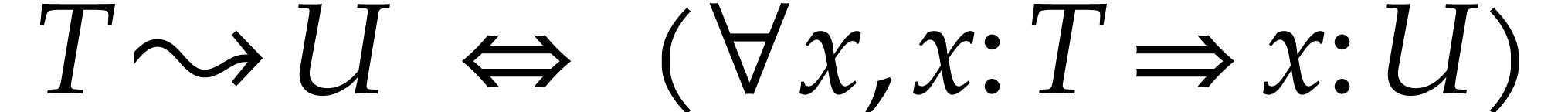
Then product, tuple and function types are required to satisfy the following conversion axioms:

We will denote by  the above formal theory for
the above formal theory for
 with incarnations of the functions and relations of the
with incarnations of the functions and relations of the  if
if  is a model for
is a model for  .
.
From the typing point of view, an environment corresponds to a finite
set 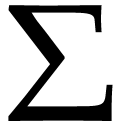 of additional hypotheses in
of additional hypotheses in  . For instance, an environment in which we have functions
. For instance, an environment in which we have functions
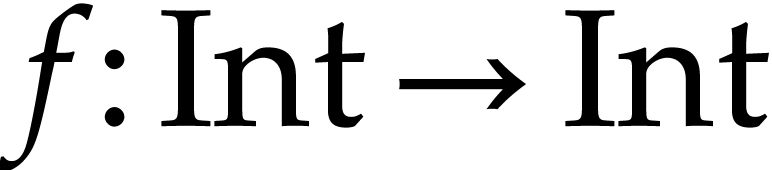 ,
,  and a converter
and a converter  simply corresponds to the set
simply corresponds to the set  .
Again, we may consider models
.
Again, we may consider models 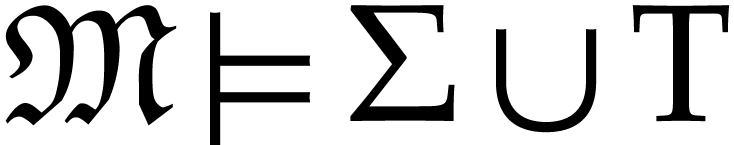 of the theory
of the theory
 enriched with
enriched with 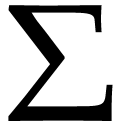 .
.
Logical types
Given a model  or
or 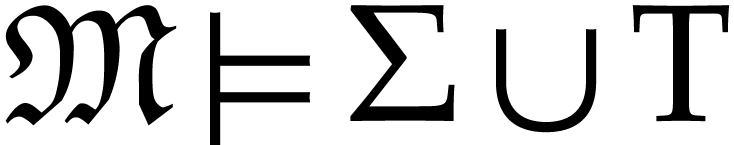 , we
say that
, we
say that 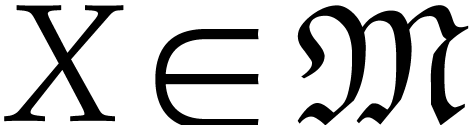 is a type if
is a type if 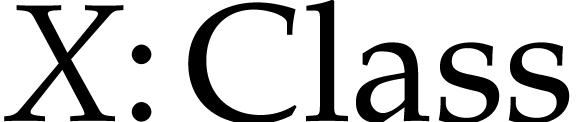 .
In that case, we call
.
In that case, we call
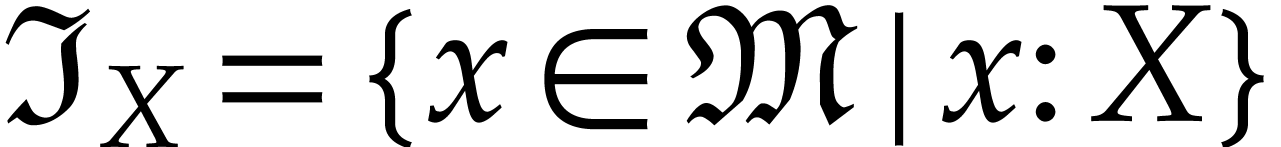
the set of instances of 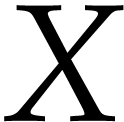 . Inversely, given a
subset
. Inversely, given a
subset  , it is natural to search for a type
, it is natural to search for a type
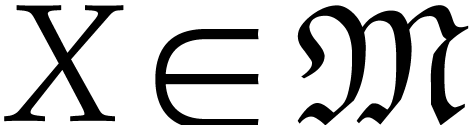 with
with 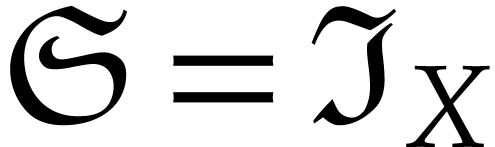 . In order to
ensure the existence of such types for simple sets, such as
. In order to
ensure the existence of such types for simple sets, such as  , it is useful to increase the expressiveness of our
language through the possibility to form so called logical types.
, it is useful to increase the expressiveness of our
language through the possibility to form so called logical types.
More precisely, let 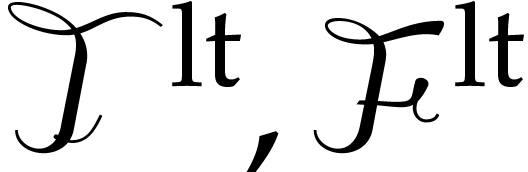 and
and  be the counterparts of
be the counterparts of  ,
,  and
and  , modulo the addition of new primitives
, modulo the addition of new primitives
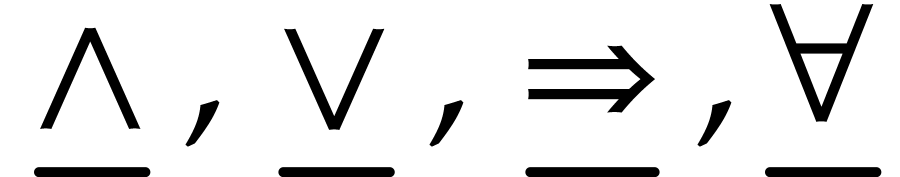 and
and  . The set
. The set  is defined in a similar way as
is defined in a similar way as  ,
modulo the following additional constructions:
,
modulo the following additional constructions:
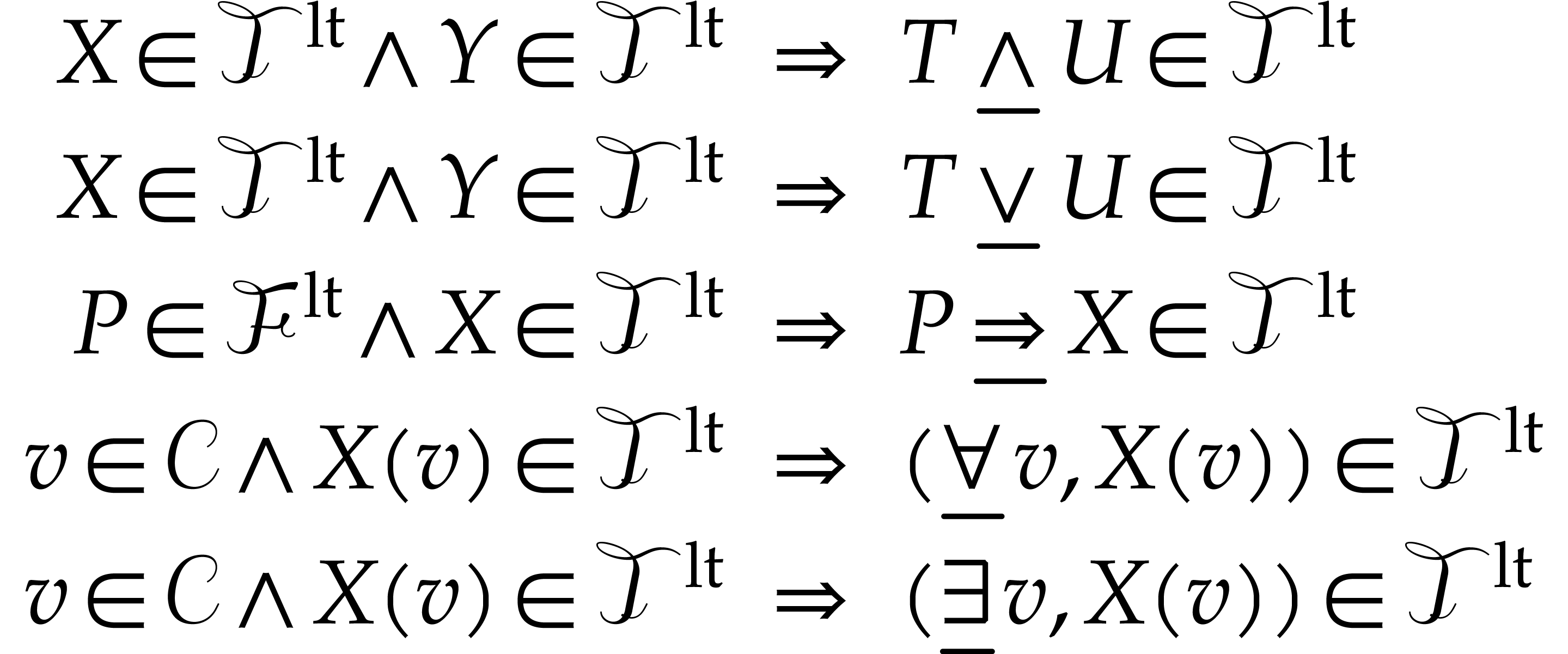
The corresponding theory  is obtained by adding
the following axioms to
is obtained by adding
the following axioms to  :
:
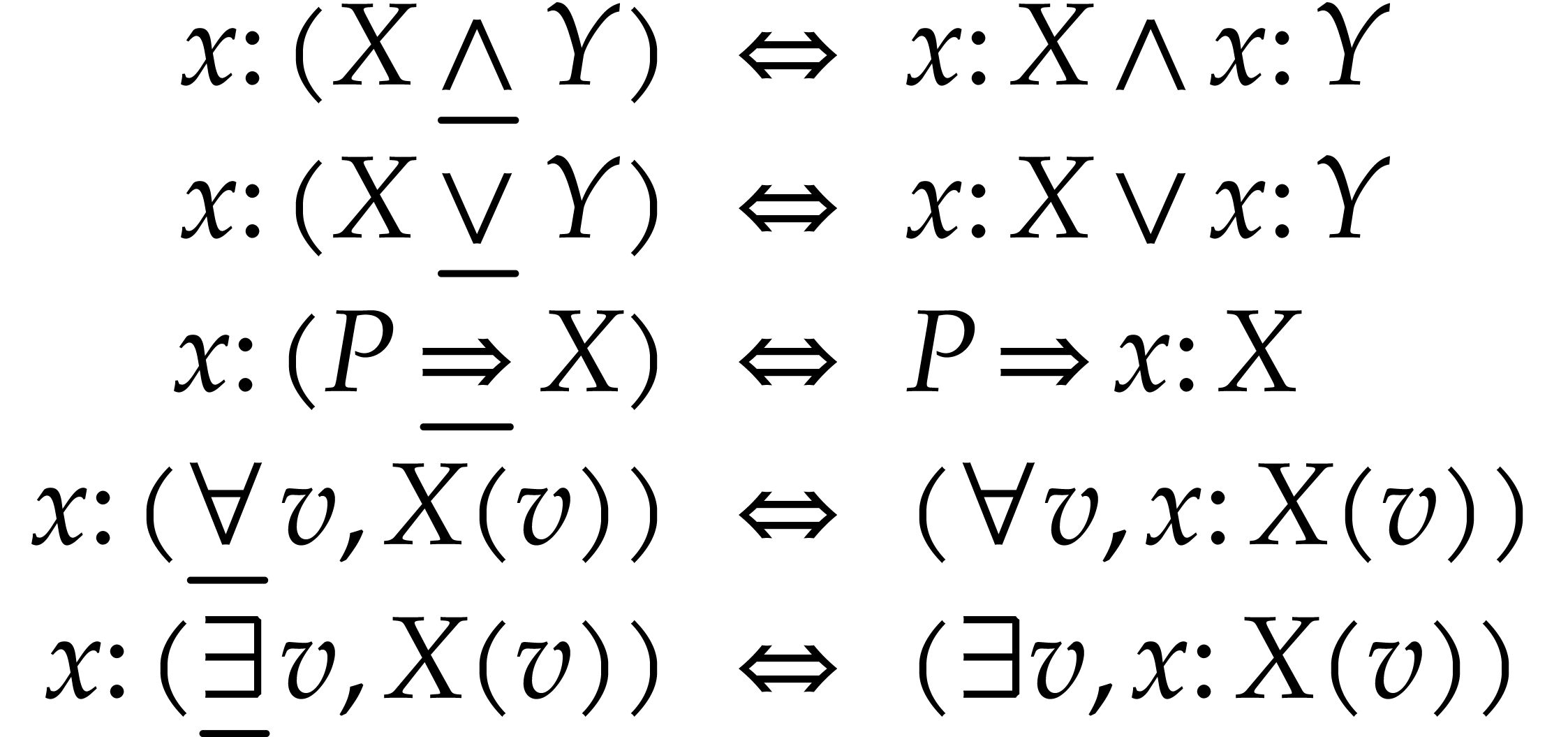
In particular,  ,
, 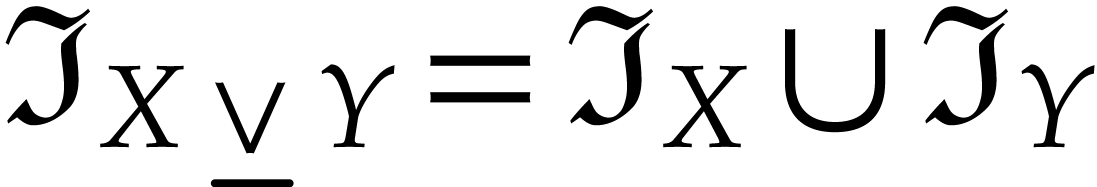 , etc.
, etc.
-
The type
 corresponds to overloading.
Indeed, an overloaded function
corresponds to overloading.
Indeed, an overloaded function 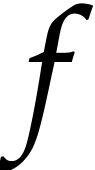 , with two
definitions
, with two
definitions 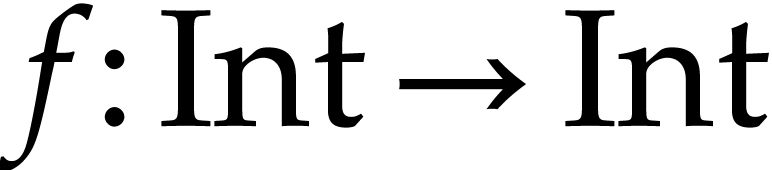 and
and  corresponds to the overloaded type
corresponds to the overloaded type  .
.
-
The type
 corresponds to an anonymous union
of
corresponds to an anonymous union
of 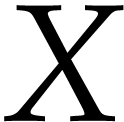 and
and  .
.
-
The type
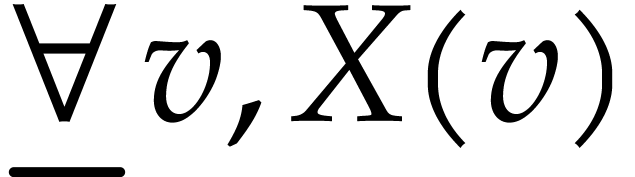 corresponds to a template type.
For instance, the C++ template template<typename
T> T square (T) gives rise to
corresponds to a template type.
For instance, the C++ template template<typename
T> T square (T) gives rise to 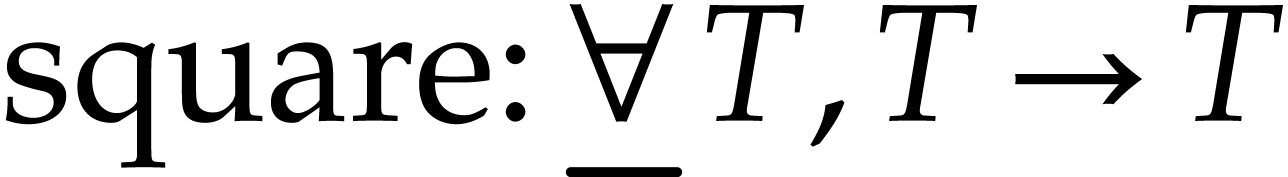 . In
. In
Mathemagix , template types are usually combined with a condition on the quantifier (see below). -
The type
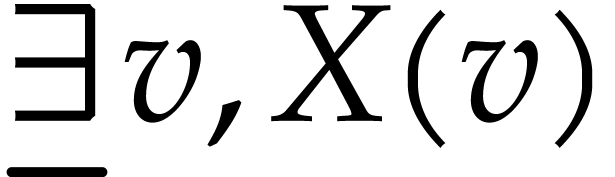 corresponds to a generic type.
For instance,
corresponds to a generic type.
For instance,  is equivalent to the
is equivalent to the  type of
type of Mathemagix . Similarly,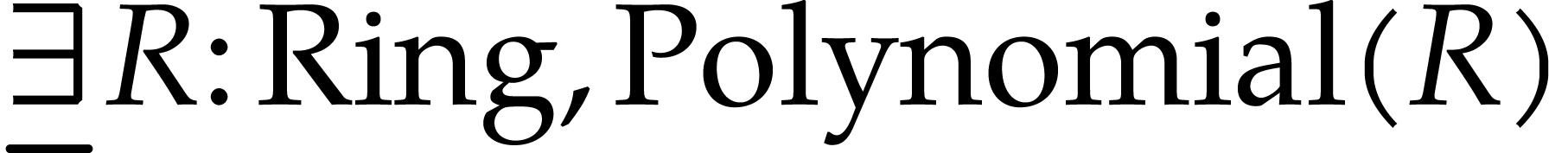 corresponds to a polynomial
over some generic ring.
corresponds to a polynomial
over some generic ring.
-
The type
 corresponds to a conditional
type. The condition usually concerns a quantifier. For instance, a
clean specification of squaring a ring element would be given by
corresponds to a conditional
type. The condition usually concerns a quantifier. For instance, a
clean specification of squaring a ring element would be given by
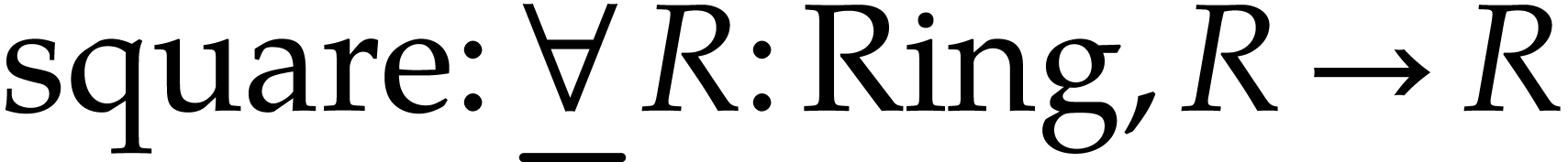 , which is really a notation for
, which is really a notation for 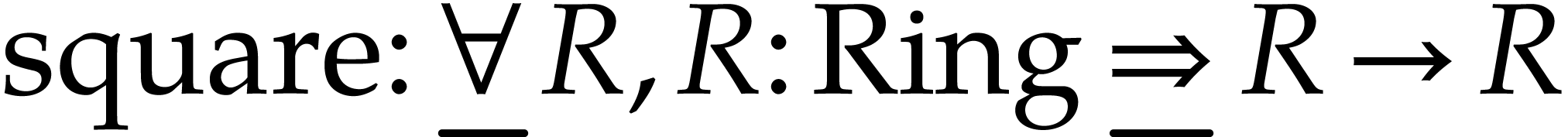 .
.
Initial models
Type resolution